题目内容
已知数列{an}（n∈N*）满足a1=1且an=an-1cos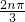
，则其前2013项的和为________．
0
分析：分别求出当n=3k，n=3k+1，n=3k+2（k∈N）时的
的值，由a1=1依次求出a2，a3，…，分析发现数列从第一项起每三项和等于0，由此求出其前2013项的和．
解答：当n=3k（k∈N）时，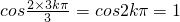
，
当n=3k+1（k∈N）时，
=
，
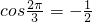当n=3k+2（k∈N）时，
=
，
由a1=1且an=an-1cos，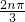
得：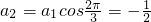
，
，
，
，
，
…
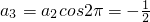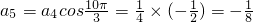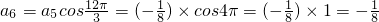由此可得从第一项起，数列{an}的每三项和为0，
而2013=671×3，所以，S2013=（a1+a2+a3）+（a4+a5+a6）+…+（a2011+a2012+a2013）=0．
故答案为0．
点评：本题考查了余弦函数值的求解，考查了求数列的和，重点考查了学生的归纳和推理能力，属中档题．
分析：分别求出当n=3k，n=3k+1，n=3k+2（k∈N）时的
的值，由a1=1依次求出a2，a3，…，分析发现数列从第一项起每三项和等于0，由此求出其前2013项的和．解答：当n=3k（k∈N）时，
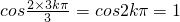，当n=3k+1（k∈N）时，
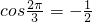=，当n=3k+2（k∈N）时，
=，由a1=1且an=an-1cos
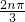，得：
，，，，，…
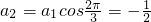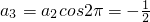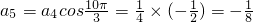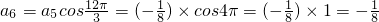由此可得从第一项起，数列{an}的每三项和为0，
而2013=671×3，所以，S2013=（a1+a2+a3）+（a4+a5+a6）+…+（a2011+a2012+a2013）=0．
故答案为0．
点评：本题考查了余弦函数值的求解，考查了求数列的和，重点考查了学生的归纳和推理能力，属中档题．
练习册系列答案
阅读快车系列答案
相关题目