Question

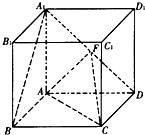（2009•泰安一模）正方体．ABCD-A₁B₁C₁D₁的棱长为l，点F、H分别为为A₁D、A₁C的中点．
（Ⅰ）证明：A₁B∥平面AFC；
（Ⅱ）证明：B₁H⊥平面AFC．

Answer 1

分析：（I）连BD交AC于点E，连EF，可得EF是△A₁BD的中位线，得EF∥A₁B，利用线面平行的判定定理即可证出A₁B∥平面AFC；
（II）连结B₁C，根据正方体的对角面A₁B₁CD为矩形，得A₁C的中点H也是B₁D的中点，因此问题转化为证明B₁D⊥平面AFC．利用正方体的性质，结合线面垂直的判定与性质证出AF⊥B₁D且AE⊥B₁D，最后根据AF、AE是平面AFC内的相交直线，可得
B₁D⊥平面AFC，由此得到B₁H⊥平面AFC．

解答：解：（Ⅰ）连结BD交AC于点E，则E为BD的中点，连结EF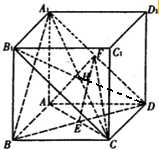
∵EF是△A₁BD的中位线，∴EF∥A₁B
∵EF?平面AFC，A₁B?平面AFC，
∴A₁B∥平面AFC；
（II）连结B₁C，在正方体ABCD-A₁B₁C₁D₁中，四边形A₁B₁CD是矩形
∵矩形A₁B₁CD中，H为A₁C的中点，∴H也是B₁D的中点
因此，要证明B₁H⊥平面AFC，即证明B₁D⊥平面AFC
∵正方体ABCD-A₁B₁C₁D₁中，A₁B₁⊥平面AA₁C₁C，AF?平面AA₁C₁C，∴AF⊥A₁B₁
又∵正方形AA₁C₁C中，AF⊥A₁D，A₁B₁∩A₁D=A₁，
∴AF⊥平面A₁B₁CD，结合B₁D?平面A₁B₁CD，得AF⊥B₁D
同理可证：AE⊥B₁D，
∵AF、AE是平面AFC内的相交直线，
∴B₁D⊥平面AFC，即B₁H⊥平面AFC

点评：本题在正方体中证明线面平行，并且探索了线面垂直的位置关系，着重考查了正方体的性质、线面垂直的判定与性质和线面平行判定定理等知识，属于中档题．