题目内容
已知每项均大于零的数列{an}中，首项a1=1且前n项的和Sn满足Sn
-Sn-1
=2
（n∈N*，且n≥2），则a81=（ ）
| Sn-1 |
| Sn |
| SnSn-1 |
分析：等式两边同除以
，可得
}是以1为首项，2为公差的等差数列，从而得到Sn=4n2-4n+1，利用n≥2时，an=Sn-Sn-1，即可求得结论．
| SnSn-1 |
| Sn |
解答：解：∵Sn
-Sn-1
=2
，
∴
-
=2（n∈N*，且n≥2），
∵a1=1，∴
=1
∴{
}是以1为首项，2为公差的等差数列
∴
=1+2（n-1）=2n-1
∴Sn=4n2-4n+1．
∴n≥2时，an=Sn-Sn-1=（4n2-4n+1）-[4（n-1）2-4（n-1）+1]=8n-8．
∴a81=8×81-8=640
故选C．
| Sn-1 |
| Sn |
| SnSn-1 |
∴
| Sn |
| Sn-1 |
∵a1=1，∴
| S1 |
∴{
| Sn |
∴
| Sn |
∴Sn=4n2-4n+1．
∴n≥2时，an=Sn-Sn-1=（4n2-4n+1）-[4（n-1）2-4（n-1）+1]=8n-8．
∴a81=8×81-8=640
故选C．
点评：本题考查数列的递推式，解题时要注意求解通项公式的方法技巧．
练习册系列答案
相关题目
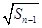－Sn－1
＝2
(n∈N*且n≥2)，则a81＝( )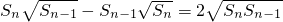
（n∈N*，且n≥2），则a81=
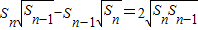（n∈N*，且n≥2），则a81=（ ）
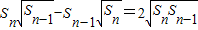（n∈N*，且n≥2），则a81=（ ）