题目内容
在△ 中,已知
中,已知 ,向量
,向量 ,
, ,且
,且 .
.
(1)求 的值;
的值;
(2)若点 在边
在边 上,且
上,且 ,
, ,求△
,求△ 的面积.
的面积.
 中,已知
中,已知 ,向量
,向量 ,
, ,且
,且 .
.(1)求
 的值;
的值;(2)若点
 在边
在边 上,且
上,且 ,
, ,求△
,求△ 的面积.
的面积.(1)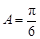 ,(2)
,(2)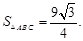
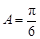 ,(2)
,(2)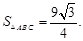
试题分析:(1)由条件
 可得
可得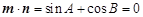 ,此时有两个解题思路:一是消元,由
,此时有两个解题思路:一是消元,由 ,
,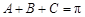 ,所以
,所以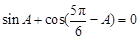 ,又
,又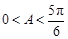 ,所以
,所以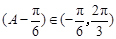 ,所以
,所以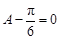 ,即
,即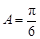 ,二是利用诱导公式转化条件,因为
,二是利用诱导公式转化条件,因为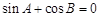 ,所以
,所以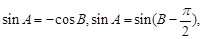 因为
因为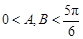 ,所以
,所以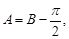 而
而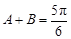 ,因此
,因此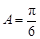 ,(2)由(1)知三角形的三个内角,所以求面积的关键在于求边,由角关系可知三边关系为
,(2)由(1)知三角形的三个内角,所以求面积的关键在于求边,由角关系可知三边关系为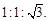 设
设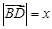 ,得
,得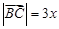 ,所以
,所以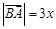 ,在△
,在△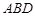 中,由余弦定理,得
中,由余弦定理,得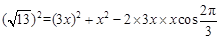 ,解得
,解得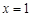 ,所以
,所以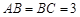 ,所以
,所以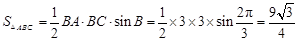 .
.试题解析:(1)由题意知
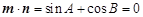 , 2分
, 2分又
 ,
,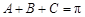 ,所以
,所以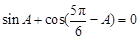 , 4分
, 4分即
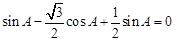 ,即
,即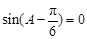 , 6分
, 6分又
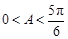 ,所以
,所以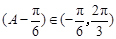 ,所以
,所以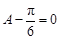 ,即
,即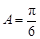 . 7分
. 7分(2)设
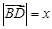 ,由
,由 ,得
,得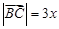 ,
,由(1)知
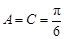 ,所以
,所以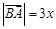 ,
,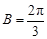 ,
,在△
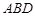 中,由余弦定理,得
中,由余弦定理,得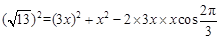 , 10分
, 10分解得
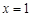 ,所以
,所以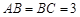 , 12分
, 12分所以
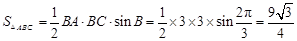 . 14分
. 14分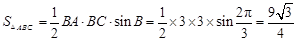 化简,余弦定理
化简,余弦定理
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
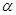 的终边经过点
的终边经过点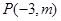 ,且
,且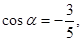
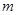 的值.(2)求
的值.(2)求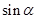 与
与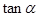 的值.
的值.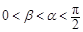 ,且
,且 ,则
,则 的值为 .
的值为 .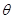 是△ABC的一个内角,且sin θcos θ=-
是△ABC的一个内角,且sin θcos θ=-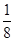 ,则sin θ-cos θ的值为( )
,则sin θ-cos θ的值为( )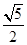
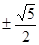
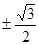
 ,则
,则 ( )
( )


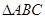 的内角
的内角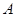 、
、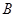 、
、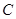 所对的边分别为
所对的边分别为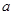 、
、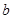 、
、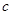 ,且
,且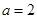 ,
,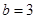 ,
,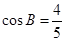 .
.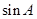 的值为 .
的值为 .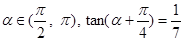 ,则
,则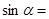 ( )
( )



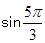 的值是( )
的值是( )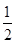
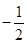
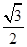
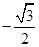
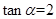 ,则
,则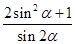 = .
= .