题目内容
14、若函数f(χ)是偶函数,且当χ<0时,有f(χ)=cos3χ+sin2χ,则当χ>0时,f(χ)的表达式为
cos3x-sin2x
.分析:由偶函数的定义,我们可以利用f(-x)=f(x),结合x<0时,f(χ)=cos3χ+sin2χ,求出当x>0时,求f(x)的解析式.
解答:解:当x>0时,-x<0
此时f(-x)=cos3(-x)+sin2(-x)
=cos3x-sin2x
故选Cos3x-sin2x
此时f(-x)=cos3(-x)+sin2(-x)
=cos3x-sin2x
故选Cos3x-sin2x
点评:本题解析的关键点是根据函数的奇偶性,求函数在对称区间上的解析式,若已知函数的奇偶性,及函数在区间[a,b]上的解析式,求对称区间[-b,-a]上的解析式,一般步骤为:取区间上任意一个数,即x∈[-b,-a],则-x∈[a,b],由区间[a,b]上的解析式,写出f(-x)的表达式,根据奇函数f(-x)=-f(x)(偶函数f(-x)=f(x))给出区间[-b,-a]上函数的解析式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
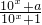 是奇函数.
是奇函数.