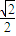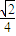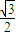题目内容
已知F为椭圆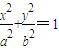 (a>b>0)的右焦点,直线l过点F且与双曲线
(a>b>0)的右焦点,直线l过点F且与双曲线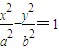 的两条渐进线l1,l2分别交于点M,N,与椭圆交于点A,B.
的两条渐进线l1,l2分别交于点M,N,与椭圆交于点A,B.(Ⅰ)若
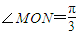 ,双曲线的焦距为4.求椭圆方程.
,双曲线的焦距为4.求椭圆方程.(Ⅱ)若
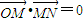 (O为坐标原点),
(O为坐标原点),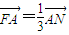 ,求椭圆的离心率e.
,求椭圆的离心率e.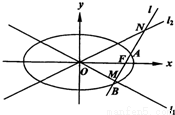
【答案】分析:(Ⅰ)由双曲线的两条渐近线的夹角以及双曲线的焦点位置可得到关于a,b的等式,再根据双曲线的焦距又可得到一个含a,b的等式,解得a,b的值,代入椭圆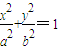 中,即可得到椭圆方程.
中,即可得到椭圆方程.
(Ⅱ)根据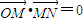 可知直线l垂直于l1,因为l1是双曲线的渐近线,可求出l1的方程,再根据l垂直于l1,就可得到l的斜率,再根据F点坐标求出直线l的方程,再由
可知直线l垂直于l1,因为l1是双曲线的渐近线,可求出l1的方程,再根据l垂直于l1,就可得到l的斜率,再根据F点坐标求出直线l的方程,再由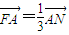 求出A点坐标,代入椭圆方程,就可得到关于a,c的齐次式,因为离心率e=
求出A点坐标,代入椭圆方程,就可得到关于a,c的齐次式,因为离心率e=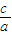 ,即可求出离心率e.
,即可求出离心率e.
解答:解:(Ⅰ)∵双曲线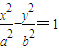 的焦点在x轴上,
的焦点在x轴上,
∴渐近线方程为y=±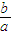 x
x
∴渐进线l1的斜率为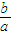
又∵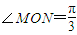 ,M,N是直线l与双曲线两条渐近线l1,l2的交点,
,M,N是直线l与双曲线两条渐近线l1,l2的交点,
∴渐进线l1的倾斜角为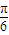 ,
,
∴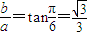 ,即
,即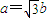
∵双曲线的焦距为4,
∴a2+b2=4.
把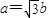 代入,得,a2=3,b2=1
代入,得,a2=3,b2=1
∴椭圆方程为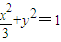
(Ⅱ)解:设椭圆的焦距为2c,则点F的坐标为(c,0)
∵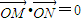 ,∴l⊥l1
,∴l⊥l1
∵直线l1的方程为y=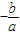 x,∴直线l的斜率为
x,∴直线l的斜率为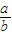 ,
,
∴直线l的方程为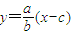
联立l1,l方程,由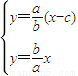 解得
解得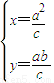
即点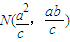
设A(x,y),由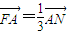 ,得
,得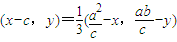
即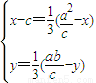 ,解得,
,解得,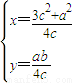
∴
∵点A在椭圆上,代入椭圆方程,得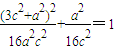
即 (3c2+a2)2+a4=16a2c2,
∴(3e2+1)2+1=16e2,即9e4-10e2+2=0
解得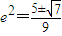
∴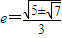
椭圆的离心率是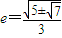
点评:本题(Ⅰ)主要考查了双曲线的渐近线方程,以及双曲线中a,b,c之间的关系的应用.(Ⅱ)考查了直线与圆锥曲线关系的判断,以及椭圆离心率的求法.
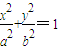 中,即可得到椭圆方程.
中,即可得到椭圆方程.(Ⅱ)根据
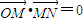 可知直线l垂直于l1,因为l1是双曲线的渐近线,可求出l1的方程,再根据l垂直于l1,就可得到l的斜率,再根据F点坐标求出直线l的方程,再由
可知直线l垂直于l1,因为l1是双曲线的渐近线,可求出l1的方程,再根据l垂直于l1,就可得到l的斜率,再根据F点坐标求出直线l的方程,再由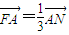 求出A点坐标,代入椭圆方程,就可得到关于a,c的齐次式,因为离心率e=
求出A点坐标,代入椭圆方程,就可得到关于a,c的齐次式,因为离心率e=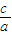 ,即可求出离心率e.
,即可求出离心率e.解答:解:(Ⅰ)∵双曲线
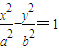 的焦点在x轴上,
的焦点在x轴上,∴渐近线方程为y=±
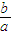 x
x∴渐进线l1的斜率为
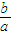
又∵
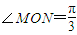 ,M,N是直线l与双曲线两条渐近线l1,l2的交点,
,M,N是直线l与双曲线两条渐近线l1,l2的交点,∴渐进线l1的倾斜角为
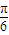 ,
,∴
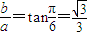 ,即
,即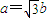
∵双曲线的焦距为4,
∴a2+b2=4.
把
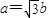 代入,得,a2=3,b2=1
代入,得,a2=3,b2=1∴椭圆方程为
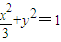
(Ⅱ)解:设椭圆的焦距为2c,则点F的坐标为(c,0)
∵
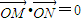 ,∴l⊥l1
,∴l⊥l1∵直线l1的方程为y=
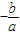 x,∴直线l的斜率为
x,∴直线l的斜率为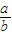 ,
,∴直线l的方程为
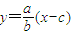
联立l1,l方程,由
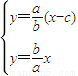 解得
解得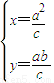
即点
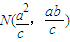
设A(x,y),由
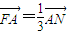 ,得
,得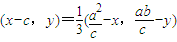
即
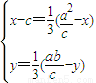 ,解得,
,解得,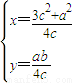
∴

∵点A在椭圆上,代入椭圆方程,得
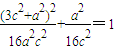
即 (3c2+a2)2+a4=16a2c2,
∴(3e2+1)2+1=16e2,即9e4-10e2+2=0
解得
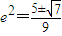
∴
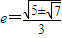
椭圆的离心率是
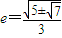
点评:本题(Ⅰ)主要考查了双曲线的渐近线方程,以及双曲线中a,b,c之间的关系的应用.(Ⅱ)考查了直线与圆锥曲线关系的判断,以及椭圆离心率的求法.

练习册系列答案
相关题目
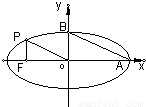
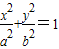 (a>b>0)的左焦点,P是椭圆上的一点,PF⊥x轴,OP∥AB(O为原点),则该椭圆的离心率是( )
(a>b>0)的左焦点,P是椭圆上的一点,PF⊥x轴,OP∥AB(O为原点),则该椭圆的离心率是( )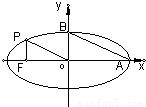
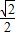
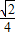

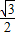
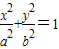 (a>b>0)的左焦点,P是椭圆上的一点,PF⊥x轴,OP∥AB(O为原点),则该椭圆的离心率是( )
(a>b>0)的左焦点,P是椭圆上的一点,PF⊥x轴,OP∥AB(O为原点),则该椭圆的离心率是( )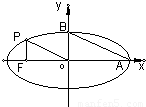
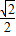
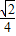

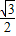
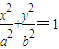 (a>b>0)的左焦点,P是椭圆上的一点,PF⊥x轴,OP∥AB(O为原点),则该椭圆的离心率是( )
(a>b>0)的左焦点,P是椭圆上的一点,PF⊥x轴,OP∥AB(O为原点),则该椭圆的离心率是( )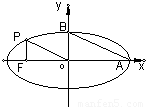
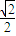
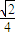

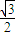
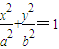 (a>b>0)的左焦点,P是椭圆上的一点,PF⊥x轴,OP∥AB(O为原点),则该椭圆的离心率是( )
(a>b>0)的左焦点,P是椭圆上的一点,PF⊥x轴,OP∥AB(O为原点),则该椭圆的离心率是( )