题目内容
类比“圆心与一条直线上的点的距离的最小值等于圆的半径,当且仅当这条直线和这个圆恰有一个公共点”.给出直线和椭圆恰有一个公共点的正确命题________.
椭圆的两个焦点到一条直线上的点的距离之和的最小值等于椭圆长轴长,当且仅当这条直线和这个椭圆恰有一个公共点.
分析:根据圆中的某些性质类比推理出椭圆中的某些性质,一般遵循“圆心到焦点”,“线到线”,“半径到焦半径”等原则,由在圆中,已知“圆心与一条直线上的点的距离的最小值等于圆的半径,当且仅当这条直线和这个圆恰有一个公共点”,是一个与切线有关的性质,由此可以类比推出椭圆中一个与切线有关的性质,由此即可得到答案.
解答:∵“圆心与一条直线上的点的距离的最小值等于圆的半径,当且仅当这条直线和这个圆恰有一个公共点”,
根据平面圆的性质可类比为椭圆的性质,则我们将得到:
“椭圆的两个焦点到一条直线上的点的距离之和的最小值等于椭圆长轴长,当且仅当这条直线和这个椭圆恰有一个公共点”
故答案为:椭圆的两个焦点到一条直线上的点的距离之和的最小值等于椭圆长轴长,当且仅当这条直线和这个椭圆恰有一个公共点.
点评:本题考查的知识点是类比推理,类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).
分析:根据圆中的某些性质类比推理出椭圆中的某些性质,一般遵循“圆心到焦点”,“线到线”,“半径到焦半径”等原则,由在圆中,已知“圆心与一条直线上的点的距离的最小值等于圆的半径,当且仅当这条直线和这个圆恰有一个公共点”,是一个与切线有关的性质,由此可以类比推出椭圆中一个与切线有关的性质,由此即可得到答案.
解答:∵“圆心与一条直线上的点的距离的最小值等于圆的半径,当且仅当这条直线和这个圆恰有一个公共点”,
根据平面圆的性质可类比为椭圆的性质,则我们将得到:
“椭圆的两个焦点到一条直线上的点的距离之和的最小值等于椭圆长轴长,当且仅当这条直线和这个椭圆恰有一个公共点”
故答案为:椭圆的两个焦点到一条直线上的点的距离之和的最小值等于椭圆长轴长,当且仅当这条直线和这个椭圆恰有一个公共点.
点评:本题考查的知识点是类比推理,类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
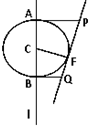 (2007•湛江二模)如图,F是定直线l外的一个定点,C是l上的动点,有下列结论:若以C为圆心,CF为半径的圆与l相交于A、B两点,过A、B分别作l的垂线与圆C过F的切线相交于点P和点Q,则必在以F为焦点,l为准线的同一条抛物线上.
(2007•湛江二模)如图,F是定直线l外的一个定点,C是l上的动点,有下列结论:若以C为圆心,CF为半径的圆与l相交于A、B两点,过A、B分别作l的垂线与圆C过F的切线相交于点P和点Q,则必在以F为焦点,l为准线的同一条抛物线上.