题目内容
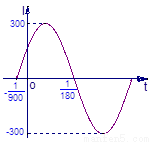
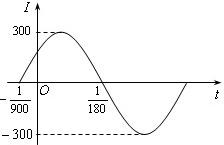
已知电流I与时间t的关系式为I=Asin(ωt+φ).(Ⅰ)右图是I=Asin(ωt+φ)(A>0,ω>0,
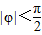 )
)在一个周期内的图象,根据图中数据求I=Asin(ωt+φ)的解析式;
(Ⅱ)如果t在任意一段
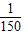 秒的时间内,电流I=Asin(ωt+φ)都能取得最大值和最小值,那么ω的最小正整数值是多少?
秒的时间内,电流I=Asin(ωt+φ)都能取得最大值和最小值,那么ω的最小正整数值是多少?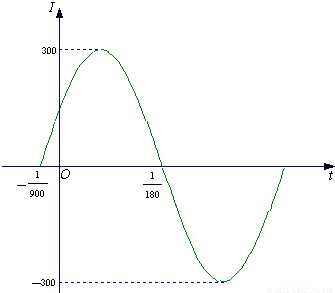
【答案】分析:(I)由已知中函数的图象,我们可以分析出函数的最大值,最小值,周期及特殊点坐标,根据函数的解析式中参数与函数性质的关系,易得到函数的解析式.
(II)由已知中如果t在任意一段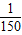 秒的时间内,电流I=Asin(ωt+φ)都能取得最大值和最小值,则函数的周期T≤
秒的时间内,电流I=Asin(ωt+φ)都能取得最大值和最小值,则函数的周期T≤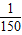 ,则易求出满足条件的ω值.
,则易求出满足条件的ω值.
解答:解:(Ⅰ)由图可知 A=300,…(1分)
设t1=-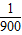 ,t2=
,t2=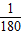 ,
,
则周期T=2(t2-t1)=2(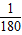 +
+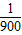 )=
)=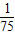 .…(4分)
.…(4分)
∴ω=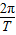 =150π. 又当t=
=150π. 又当t=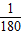 时,I=0,即sin(150π•
时,I=0,即sin(150π•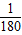 +φ)=0,
+φ)=0,
而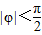 ,∴φ=
,∴φ=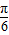 .…(6分)
.…(6分)
故所求的解析式为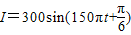 .…(8分)
.…(8分)
(Ⅱ)依题意,周期T≤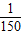 ,即
,即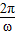 ≤
≤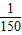 ,(ω>0)
,(ω>0)
∴ω≥300π>942,又ω∈N*故最小正整数ω=943.…(12分)
点评:本题考查的知识点是由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数的最值,其中(I)的关键是熟练掌握函数的解析式中参数与函数性质的关系,(II)的关键是根据已知条件得到函数的周期T≤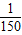 ,进而构造关于ω的不等式.
,进而构造关于ω的不等式.
(II)由已知中如果t在任意一段
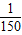 秒的时间内,电流I=Asin(ωt+φ)都能取得最大值和最小值,则函数的周期T≤
秒的时间内,电流I=Asin(ωt+φ)都能取得最大值和最小值,则函数的周期T≤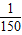 ,则易求出满足条件的ω值.
,则易求出满足条件的ω值.解答:解:(Ⅰ)由图可知 A=300,…(1分)
设t1=-
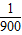 ,t2=
,t2=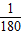 ,
,则周期T=2(t2-t1)=2(
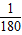 +
+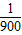 )=
)=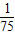 .…(4分)
.…(4分)∴ω=
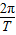 =150π. 又当t=
=150π. 又当t=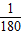 时,I=0,即sin(150π•
时,I=0,即sin(150π•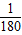 +φ)=0,
+φ)=0,而
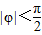 ,∴φ=
,∴φ=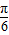 .…(6分)
.…(6分)故所求的解析式为
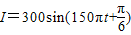 .…(8分)
.…(8分)(Ⅱ)依题意,周期T≤
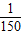 ,即
,即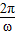 ≤
≤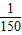 ,(ω>0)
,(ω>0)∴ω≥300π>942,又ω∈N*故最小正整数ω=943.…(12分)
点评:本题考查的知识点是由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数的最值,其中(I)的关键是熟练掌握函数的解析式中参数与函数性质的关系,(II)的关键是根据已知条件得到函数的周期T≤
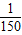 ,进而构造关于ω的不等式.
,进而构造关于ω的不等式. 
练习册系列答案
相关题目
 已知电流I与时间t的关系式为I=Asin(ωt+φ).
已知电流I与时间t的关系式为I=Asin(ωt+φ).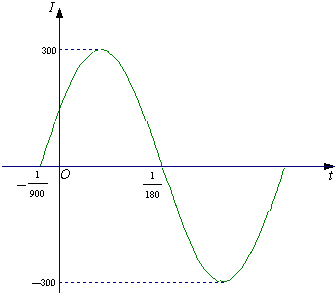 已知电流I与时间t的关系式为I=Asin(ωt+φ).
已知电流I与时间t的关系式为I=Asin(ωt+φ).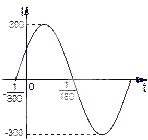 已知电流I与时间t的关系式为I=Asin(ωx+φ).
已知电流I与时间t的关系式为I=Asin(ωx+φ).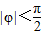 )在一个周期内的图象,根据图中数据求I=Asin(ωt+φ)的解析式;
)在一个周期内的图象,根据图中数据求I=Asin(ωt+φ)的解析式;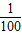 秒的时间内,电流I=Asin(ωt+φ)都能取得最大值和最小值,那么ω的最小正整数值是多少?
秒的时间内,电流I=Asin(ωt+φ)都能取得最大值和最小值,那么ω的最小正整数值是多少?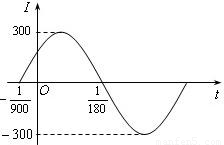
 。
。 )在一个周期内的图象,根据图中数据求
)在一个周期内的图象,根据图中数据求 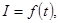 求
求 的单调递增区间
的单调递增区间