题目内容
设直线kx-y+1=0被圆O:x2+y2=4所截弦的中点的轨迹为C,则曲线C与直线x+y-1=0的位置关系为
- A.相离
- B.相切
- C.相交
- D.不确定
C
分析:设C上任意一点的坐标为A(x,y),由 ×k=-1,求出k后代入直线kx-y+1=0求得曲线C的方程,由圆心(0,
×k=-1,求出k后代入直线kx-y+1=0求得曲线C的方程,由圆心(0, )到直线x+y-1=0的距离小于半径得到曲线C与直线x+y-1=0相交.
)到直线x+y-1=0的距离小于半径得到曲线C与直线x+y-1=0相交.
解答:弦的中点的轨迹为C,设C上任意一点的坐标为A( x,y ),则由弦的性质得 OA垂直于直线kx-y+1=0,
∴ ×k=-1,即 k=
×k=-1,即 k=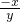 .又点A( x,y )还在直线kx-y+1=0上,
.又点A( x,y )还在直线kx-y+1=0上,
∴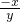 •x-y+1=0,x2+
•x-y+1=0,x2+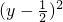 =
= ,故曲线C表示以(0,
,故曲线C表示以(0, )为圆心,以
)为圆心,以 为半径的圆.
为半径的圆.
∵圆心(0, )到直线x+y-1=0的距离等于
)到直线x+y-1=0的距离等于  =
= <
< (半径),
(半径),
故曲线C与直线x+y-1=0相交,
故选C.
点评:本题考查求点的轨迹方程的求法,直线和圆相交的性质,求曲线C的轨迹方程是解题的关键.
分析:设C上任意一点的坐标为A(x,y),由
 ×k=-1,求出k后代入直线kx-y+1=0求得曲线C的方程,由圆心(0,
×k=-1,求出k后代入直线kx-y+1=0求得曲线C的方程,由圆心(0, )到直线x+y-1=0的距离小于半径得到曲线C与直线x+y-1=0相交.
)到直线x+y-1=0的距离小于半径得到曲线C与直线x+y-1=0相交.解答:弦的中点的轨迹为C,设C上任意一点的坐标为A( x,y ),则由弦的性质得 OA垂直于直线kx-y+1=0,
∴
 ×k=-1,即 k=
×k=-1,即 k=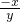 .又点A( x,y )还在直线kx-y+1=0上,
.又点A( x,y )还在直线kx-y+1=0上,∴
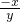 •x-y+1=0,x2+
•x-y+1=0,x2+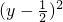 =
= ,故曲线C表示以(0,
,故曲线C表示以(0, )为圆心,以
)为圆心,以 为半径的圆.
为半径的圆.∵圆心(0,
 )到直线x+y-1=0的距离等于
)到直线x+y-1=0的距离等于  =
= <
< (半径),
(半径),故曲线C与直线x+y-1=0相交,
故选C.
点评:本题考查求点的轨迹方程的求法,直线和圆相交的性质,求曲线C的轨迹方程是解题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
设直线kx-y+1=0被圆O:x2+y2=4所截弦的中点的轨迹为C,则曲线C与直线x+y-1=0的位置关系为( )
| A、相离 | B、相切 | C、相交 | D、不确定 |
 所截弦的中点的轨迹为C,则曲线C与直线
所截弦的中点的轨迹为C,则曲线C与直线