Question

（本小题满分12分）

某企业科研课题组计划投资研发一种新产品，根据分析和预测，能获得10万元～1000万元的投资收益.企业拟制定方案对课题组进行奖励，奖励方案为：奖金y(单位：万元)随投资收益x(单位：万元)的增加而增加，且奖金不超过9万元，同时奖金也不超过投资收益的20%，并用函数y= f(x)模拟这一奖励方案.

（Ⅰ）试写出模拟函数y= f(x)所满足的条件；

（Ⅱ）试分析函数模型y= 4lgx-3是否符合奖励方案的要求？并说明你的理由.

 

Answer 1

【答案】

解：（Ⅰ）由题意，模拟函数y=f(x)满足的条件是：

（1）   f(x)在［10，1000］上是增函数；（2）f(x)≤9；（3）f(x)≤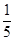x.……（3分）

(Ⅱ)对于y=4 lg x-3,显然它在［10，1000］上是增函数，满足条件（1），……（4分）

又当10≤x≤1000时，4lg10-3≤y≤4lg1000-3,即y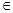［1，9］，从而满足条件（2）.（5分）

下面证明：f(x)≤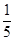x，即4lg x-3≤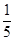x对于x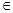［10，1000］恒成立. ……（6分）

令g(x)= 4lgx-3-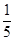x(10≤x≤1000),则g′(x)= 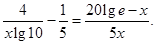…（8分）

∵e＜

∴20lge-x＜0，∴g′(x) ＜0对于x 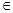［10，1000］恒成立.

∴g(x)在［10，1000］上是减函数……………………………（10分）

∴g(x)在［10，1000］时，g (x)≤g(10=4lg10-3-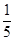×10=-1＜0，

即4lg x-3-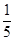x≤0，即4lg x-3≤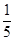x对于x 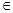［10，1000］恒成立.从而满足条件（3）.

故函数模型y=4lgx-3符合奖励方案的要求. …………………（12分）

 

【解析】略