题目内容
求证:当a、b、c为正数时,(a+b+c)(| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
分析:不等式的左边即3+
+
+
+
+
+
,由均值不等式证得此式大于或等于9.
| b |
| a |
| a |
| b |
| c |
| a |
| a |
| c |
| c |
| b |
| b |
| c |
解答:证明:当a、b、c为正数时,(a+b+c)(
+
+
)=1+
+
+
+1+
+
+
+1
=3+
+
+
+
+
+
.
由均值不等式得
+
≥2,
+
≥2,
+
≥2,
故有 3+
+
+
+
+
+
≥3+2+2+2=9,当且仅当正数a、b、c 全部相等时,等号成立.
故 (a+b+c)(
+
+
)≥9 成立.
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| b |
| a |
| c |
| a |
| a |
| b |
| c |
| b |
| a |
| c |
| b |
| c |
=3+
| b |
| a |
| a |
| b |
| c |
| a |
| a |
| c |
| c |
| b |
| b |
| c |
由均值不等式得
| b |
| a |
| a |
| b |
| c |
| a |
| a |
| c |
| c |
| b |
| b |
| c |
故有 3+
| b |
| a |
| a |
| b |
| c |
| a |
| a |
| c |
| c |
| b |
| b |
| c |
故 (a+b+c)(
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
点评:本题考查应用基本不等式证明不等式,注意检验等号成立的条件,式子的变形是解题的关键.

练习册系列答案
相关题目
 +
+ +
+ )≥9.
)≥9. +
+ +
+ )≥9
)≥9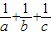 )≥9.
)≥9.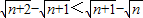 .
.