题目内容
（2013•渭南二模）若函数y=f（x）（x∈R）满足f（x+1）=f（x-1），且x∈[-1，1]时，f（x）=1-x2，函数g（x）=
，则函数h（x）=f（x）-g（x）在区间[-5，5]内的零点的个数为（ ）
|
分析：根据条件可得f（x）是周期函数，T=2，h（x）=f（x）-g（x）=0，则f（x）=g（x），在同一坐标系中作y=f（x）和y=g（x）图象，由图象可得结论．
解答：解：由题意f（1+x）=f（x-1）⇒f（x+2）=f（x），故f（x）是周期函数，T=2，
令h（x）=f（x）-g（x）=0，则f（x）=g（x），在同一坐标系中作y=f（x）和y=g（x）图象，如图所示：
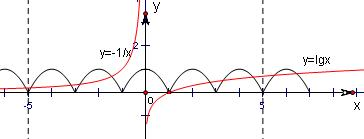
故在区间[-5，5]内，函数y=f（x）和y=g（x）图象的交点有8个，
则函数h（x）=f（x）-g（x）在区间[-5，5]内的零点的个数为8．
故选C．
令h（x）=f（x）-g（x）=0，则f（x）=g（x），在同一坐标系中作y=f（x）和y=g（x）图象，如图所示：
故在区间[-5，5]内，函数y=f（x）和y=g（x）图象的交点有8个，
则函数h（x）=f（x）-g（x）在区间[-5，5]内的零点的个数为8．
故选C．
点评：本题考查函数零点的定义，体现了数形结合的数学思想，在同一坐标系中作y=f（x）和y=g（x）图象，是解题的关键．
练习册系列答案
相关题目
（2013•渭南二模）某几何体的主视图与俯视图如图所示，左视图与主视图相同，且图中的四边形都是边长为2的正方形，两条虚线互相垂直，则该几何体的体积是（ ）