题目内容
已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R).
(1)求证:不论m取什么实数,直线l与圆C恒交于两点;
(2)求直线被圆C截得的弦长最小时直线l的方程.
(1)求证:不论m取什么实数,直线l与圆C恒交于两点;
(2)求直线被圆C截得的弦长最小时直线l的方程.
(1)见解析(2)2x-y-5=0.
(1)证明:直线l的方程整理得(x+y-4)+m(2x+y-7)=0,∵m∈R,∴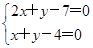
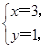 也就是直线l恒过定点A(3,1).由于|AC|=
也就是直线l恒过定点A(3,1).由于|AC|=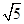 <5(半径),∴点A(3,1)在圆C内,故直线l与圆C恒交于两点.
<5(半径),∴点A(3,1)在圆C内,故直线l与圆C恒交于两点.
(2)解:弦长最小时,直线l⊥AC,而kAC=-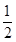 ,故此时直线l的方程为2x-y-5=0.
,故此时直线l的方程为2x-y-5=0.
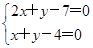
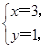 也就是直线l恒过定点A(3,1).由于|AC|=
也就是直线l恒过定点A(3,1).由于|AC|=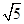 <5(半径),∴点A(3,1)在圆C内,故直线l与圆C恒交于两点.
<5(半径),∴点A(3,1)在圆C内,故直线l与圆C恒交于两点.(2)解:弦长最小时,直线l⊥AC,而kAC=-
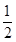 ,故此时直线l的方程为2x-y-5=0.
,故此时直线l的方程为2x-y-5=0.
练习册系列答案
相关题目
 :
: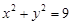 ,点
,点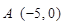 ,直线
,直线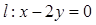 .
.
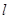 垂直的直线方程;
垂直的直线方程; 上(
上(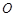 为坐标原点),存在定点
为坐标原点),存在定点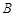 (不同于点
(不同于点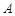 ),满足:对于圆
),满足:对于圆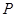 ,都有
,都有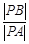 为一常数,试求出所有满足条件的点
为一常数,试求出所有满足条件的点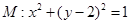 ,设点
,设点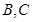 是直线
是直线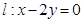 上的两点,它们的横坐标分别是
上的两点,它们的横坐标分别是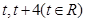 ,点
,点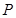 在线段
在线段 上,过
上,过 的切线
的切线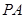 ,切点为
,切点为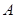 .
.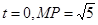 ,求直线
,求直线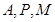 三点的圆的圆心是
三点的圆的圆心是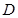 ,求线段
,求线段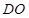 (
(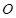 为坐标原点)长的最小值
为坐标原点)长的最小值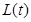 .
.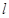 将圆
将圆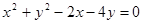 平分且不通过第四象限,则
平分且不通过第四象限,则



 )作圆O:x2+y2=r2(r>0)的切线,切点为D,且|QD|=4.
)作圆O:x2+y2=r2(r>0)的切线,切点为D,且|QD|=4. =
= +
+ ,求|
,求|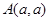 可作圆
可作圆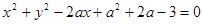 的两条切线,则实数
的两条切线,则实数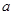 的取值范围为 .
的取值范围为 .