题目内容
已知f（x）是定义在R上的增函数，对x∈R有f（x）＞0，且f（5）=1，设F（x）=f（x）+
，讨论F （x）的单调性，并证明你的结论．
解：在R上任取x1、x2，设x1＜x2，
∴f（x2）＞f（x1），
=
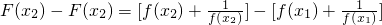
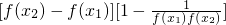
∵f（x）是R上的增函数，且f（5）=1，
∴当x＜5时0＜f（x）＜1，而当x＞5时f（x）＞1；
①若x1＜x2＜5，则0＜f（x1）＜f（x2）＜1，
∴
＜0，
∴F（x2）＜F（x1）；
②若x2＞x1＞5，则f（x2）＞f（x1）＞1，
∴f（x1）f（x2）＞1
∴
＞0
∴F（x2）＞F（x1）
综上，F（x）在（-∞，5）为减函数，在（5，+∞）为增函数
分析：这是抽角函数的单调性问题，应该用单调性定义解决．对差的符号进行判断时要注意根据其形式选择判断的方式．
点评：本题考点是抽象函数及其应用，考查抽象函数单调性的证明，对于抽象函数的单调性的判断仍然要紧扣单调性的定义，结合题目中所给性质和相应的条件，对任意x1、x2在所给区间内比较f（x2）-f（x1）与0的大小，或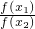
的大小．有时根据需要，需作适当的变形：如
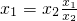，x1=x2+x1-x2
∴f（x2）＞f（x1），
=
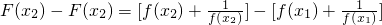
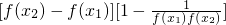
∵f（x）是R上的增函数，且f（5）=1，
∴当x＜5时0＜f（x）＜1，而当x＞5时f（x）＞1；
①若x1＜x2＜5，则0＜f（x1）＜f（x2）＜1，
∴
＜0，∴F（x2）＜F（x1）；
②若x2＞x1＞5，则f（x2）＞f（x1）＞1，
∴f（x1）f（x2）＞1
∴
＞0∴F（x2）＞F（x1）
综上，F（x）在（-∞，5）为减函数，在（5，+∞）为增函数
分析：这是抽角函数的单调性问题，应该用单调性定义解决．对差的符号进行判断时要注意根据其形式选择判断的方式．
点评：本题考点是抽象函数及其应用，考查抽象函数单调性的证明，对于抽象函数的单调性的判断仍然要紧扣单调性的定义，结合题目中所给性质和相应的条件，对任意x1、x2在所给区间内比较f（x2）-f（x1）与0的大小，或
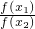的大小．有时根据需要，需作适当的变形：如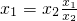，x1=x2+x1-x2 
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目