题目内容
以下有四种说法:(1)若p∨q为真,p∧q为假,则p与q必为一真一假;
(2)若数列{an}的前n项和为Sn=n2+n+1,n∈N*,则an=2n,n∈N*;
(3)若f′(x)=0,则f(x)在x=x处取得极值;
(4)由变量x和y的数据得到其回归直线方程
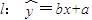 ,则l一定经过点
,则l一定经过点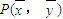 .
.以上四种说法,其中正确说法的序号为 .
【答案】分析:利用复合命题真假与简单命题真假之间的关系可以判断(1)的正确性,利用数列前n项和与通项的关系可以求出(2)中数列的通项公式应为分段函数的形式,利用函数的极值与导函数的关系,可以判断(3)的正确性,根据回归直线过样本点的中心可以确定出(4)的正确性.
解答:解:若p∨q为真,p∧q为假,则可以判断出p,q一真一假,故(1)正确;
若数列{an}的前n项和为Sn=n2+n+1,n∈N*,则a1=S1=3≠2×1,或者可以求出 ,故(2)错误;
,故(2)错误;
考虑f(x)=x3,则f′(0)=0,但是f(x)在x=0处没有极值,故(3)错误;
回归直线一定经过样本点的中心,可知(4)正确.
故答案为:(1),(4).
点评:本题考查命题真假的判断,考查学生对一些数学问题的理解和把握能力,正确解决本题需要综合用到数列、函数的极值与导数之间的联系、复合命题真假的判断方法、回归直线过样本点的性质.考查学生的转化与化归思想.
解答:解:若p∨q为真,p∧q为假,则可以判断出p,q一真一假,故(1)正确;
若数列{an}的前n项和为Sn=n2+n+1,n∈N*,则a1=S1=3≠2×1,或者可以求出
 ,故(2)错误;
,故(2)错误;考虑f(x)=x3,则f′(0)=0,但是f(x)在x=0处没有极值,故(3)错误;
回归直线一定经过样本点的中心,可知(4)正确.
故答案为:(1),(4).
点评:本题考查命题真假的判断,考查学生对一些数学问题的理解和把握能力,正确解决本题需要综合用到数列、函数的极值与导数之间的联系、复合命题真假的判断方法、回归直线过样本点的性质.考查学生的转化与化归思想.

练习册系列答案
相关题目

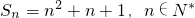 ,则
,则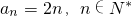 ;
;