题目内容
已知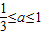 ,若f(x)=ax2-2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a),求g(a)的函数表达式.
,若f(x)=ax2-2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a),求g(a)的函数表达式.
【答案】分析:f(x)=ax2-2x+1的对称轴为x=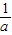 ,由
,由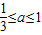 ,知1
,知1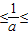 3,所以f(x)在[1,3]上,N(a)=f(
3,所以f(x)在[1,3]上,N(a)=f(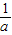 )=1-
)=1-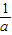 .由a的符号进行分类讨论,能求出g(a)的解析式.
.由a的符号进行分类讨论,能求出g(a)的解析式.
解答:解:f(x)=ax2-2x+1的对称轴为x= ,
,
∵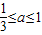 ,∴1
,∴1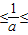 3,
3,
∴f(x)在[1,3]上,N(a)=f(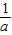 )=1-
)=1-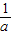 .
.
∵f(x)=ax2-2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),
∴①当1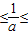 2,即
2,即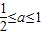 时,
时,
M(a)=f(3)=9a-5,N(a)=f(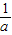 )=1-
)=1-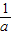 .
.
g(a)=M(a)-N(a)=9a+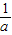 -6.
-6.
②当2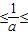 3,即
3,即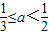 时,
时,
M(a)=f(1)=a-1,N(a)=f(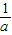 )=1-
)=1-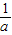 .
.
g(a)=M(a)-N(a)=a+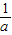 -2.
-2.
∴g(a)=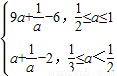 .
.
点评:本题考查函数的解析式的求法,解题时要认真审题,仔细解答,注意分类讨论思想的合理运用.
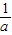 ,由
,由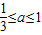 ,知1
,知1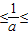 3,所以f(x)在[1,3]上,N(a)=f(
3,所以f(x)在[1,3]上,N(a)=f(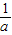 )=1-
)=1-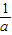 .由a的符号进行分类讨论,能求出g(a)的解析式.
.由a的符号进行分类讨论,能求出g(a)的解析式.解答:解:f(x)=ax2-2x+1的对称轴为x=
 ,
,∵
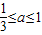 ,∴1
,∴1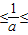 3,
3,∴f(x)在[1,3]上,N(a)=f(
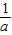 )=1-
)=1-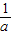 .
.∵f(x)=ax2-2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),
∴①当1
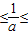 2,即
2,即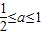 时,
时,M(a)=f(3)=9a-5,N(a)=f(
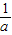 )=1-
)=1-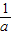 .
.g(a)=M(a)-N(a)=9a+
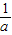 -6.
-6.②当2
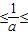 3,即
3,即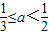 时,
时,M(a)=f(1)=a-1,N(a)=f(
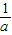 )=1-
)=1-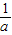 .
.g(a)=M(a)-N(a)=a+
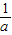 -2.
-2.∴g(a)=
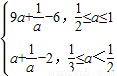 .
.点评:本题考查函数的解析式的求法,解题时要认真审题,仔细解答,注意分类讨论思想的合理运用.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 若f(x)>3,则x的取值范围是( )
若f(x)>3,则x的取值范围是( )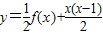 的反函数为p(x),t(x)=p(x)(1-x),求函数t(x)的最大值;
的反函数为p(x),t(x)=p(x)(1-x),求函数t(x)的最大值;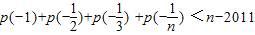 恒成立?若存在,请找出一个满足条件的N的值,并给以说明;若不存在,请说明理由.
恒成立?若存在,请找出一个满足条件的N的值,并给以说明;若不存在,请说明理由. ,若f(x)=ax2-2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),记g(a)=M(a)-N(a).
,若f(x)=ax2-2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),记g(a)=M(a)-N(a). 都有kg(a)-1<0成立,求实数k的取值范围.
都有kg(a)-1<0成立,求实数k的取值范围. 若f(x)>3,则x的取值范围是( )
若f(x)>3,则x的取值范围是( )