题目内容
下列命题:
①幂函数都具有奇偶性;
②命题P:?x0∈[-1,1],满足x02+x0+1>a,使命题P为真的实数a的取值范围为a<3;
③代数式sinα+sin(
+α)+sin(
+α)的值与角a有关;
④将函数f(x)=3sin(2x-
)的图象向左平移
个单位长度后得到的图象所对应的函数是奇函数;
⑤已知数列{an}满足:a1=m,a2=n,an+2=an+1-an(n∈N),记Sn=a1+a2+…an,则S2011=m;
其中正确的命题的序号是
①幂函数都具有奇偶性;
②命题P:?x0∈[-1,1],满足x02+x0+1>a,使命题P为真的实数a的取值范围为a<3;
③代数式sinα+sin(
| 2π |
| 3 |
| 4π |
| 3 |
④将函数f(x)=3sin(2x-
| π |
| 3 |
| π |
| 3 |
⑤已知数列{an}满足:a1=m,a2=n,an+2=an+1-an(n∈N),记Sn=a1+a2+…an,则S2011=m;
其中正确的命题的序号是
②⑤
②⑤
(请把正确命题的序号全部写出来)分析:列举反例,可得命题①为假;利用函数成立问题的处理方法,可以判断②的正误;根据特殊角三角函数值,及两角和的正弦值,可以判断③的对错;利用函数平移变换及三角函数的奇偶性的判断方法,可以判断④的对错;根据数列的分组求和法,利用数列各项的变化趋势,可以得到⑤正误,进而得到答案.
解答:解:①幂函数y=x
,定义域为[0,+∞),非奇非偶,故①不正确;
②当x0∈[-1,1]时,x02+x0+1∈[
,3]
∴?x0∈[-1,1],满足x02+x0+1>a,使命题P为真的实数a的取值范围为a<3为真命题;
③∵sinα+sin(
+α)+sin(
+α)=sinα+
cosα-
sinα-
cosα-
sinα=0恒成立,
∴代数式sinα+sin(
+α)+sin(
+α)的值与角α有关为假命题;
④将函数f(x)=3sin(2x-
)的图象向左平移
个单位长度后得到的图象所对应的函数是f(x)=3sin(2x+
),是非奇非偶函数,故④为假命题;
⑤∵数列{an}满足:a1=m,a2=n,an+2=an+1-an(n∈N),∴a3=n-m,a4=-m,a5=-n,a6=m-n,a7=m,a8=n,…
∴数列{an}的项以6为周期,呈周期性变化,且a1+a2+a3+a4+a5+a6=0,∴S2011=a1+a2+…+a2011=a1=m
故⑤为真命题
故答案为:②⑤
| 1 |
| 2 |
②当x0∈[-1,1]时,x02+x0+1∈[
| 3 |
| 4 |
∴?x0∈[-1,1],满足x02+x0+1>a,使命题P为真的实数a的取值范围为a<3为真命题;
③∵sinα+sin(
| 2π |
| 3 |
| 4π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
∴代数式sinα+sin(
| 2π |
| 3 |
| 4π |
| 3 |
④将函数f(x)=3sin(2x-
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
⑤∵数列{an}满足:a1=m,a2=n,an+2=an+1-an(n∈N),∴a3=n-m,a4=-m,a5=-n,a6=m-n,a7=m,a8=n,…
∴数列{an}的项以6为周期,呈周期性变化,且a1+a2+a3+a4+a5+a6=0,∴S2011=a1+a2+…+a2011=a1=m
故⑤为真命题
故答案为:②⑤
点评:本题考查的知识点是命题的真假判断与应用,存在量词,数列递推式,两角和与差的正弦函数,函数y=Asin(ωx+φ)的图象变换,其中熟练掌握这些基本的知识点是解答此类问题的根本.

练习册系列答案
相关题目
 ;(2)幂函数的图像不可能是一条直线;
;(2)幂函数的图像不可能是一条直线; 时,函数
时,函数 的图像是一条直线;(4)幂函数
的图像是一条直线;(4)幂函数 时,是增函数;
时,是增函数; 时,在第一象限内函数值随
时,在第一象限内函数值随 值的增大而减少。其中正确的命题序号为
值的增大而减少。其中正确的命题序号为 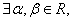
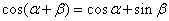 ;
;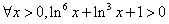 ;
;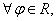 函数
函数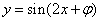 都不是偶函数;
都不是偶函数; 使
使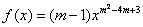 是幂函数,且在
是幂函数,且在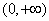 上递减.
上递减.