题目内容

(16)设函数f(x)=,点A0表示坐标原点，点An(n，f(n))(n∈N*).若向量

θn是与的夹角(其中=(1，0))，

 

设Sn=tanθl+tanθ2+…+tanθn，则Sn=_____________.

1

解析：

 

∴an=（［f(k)-f(k-1)］）=(n,f(n)),∵θn是an与=(1,0)的夹角. 

 

∴cosθn=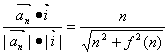  ∴tanθn=

 

 

∴Sn=(1-)+(-)+()=1-

 

∴Sn=1

 


练习册系列答案
相关题目
（2007•湖北模拟）设函数f(x)=
a
•
b
+m+m，
a
=(2，-cosωx)，
b
=(sinωx，-2)（其中ω＞0，m∈R），且f（x）的图象在y轴右侧的第一个最高点的横坐标为2．
（1）求ω；
（2）若f（x）在区间[8，16]上最大值为3，求m的值．
设函数f(x)=
x
x+2
(x＞0)，观察：f1(x)=f(x)=
x
x+2
，f2(x)=f[f1(x)]=
x
3x+4
，f3(x)=f[f2(x)]=
x
7x+8
f4(x)=f[f3(x)]=
x
15x+16

------根据以上事实，由归纳推理可得：当n∈N+且n＞1时，fn（x）=
x
(2n-1)x+2n
x
(2n-1)x+2n
．
设函数f(x)=sin(ωx+?)(ω＞0，0＜?＜
π
2
)．若将f（x）的图象沿x轴向右平移
1
6
个单位长度，得到的图象经过坐标原点；若将f（x）的图象上所有的点的横坐标缩短到原来的
1
2
倍（纵坐标不变），得到的图象经过点(
1
6
，1)，则（　　）
A、ω=π，?=
π
6
B、ω=2π，?=
π
3
C、ω=
3π
4
，?=
π
8
D、适合条件的ω，?不存在

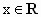(2006湖北，16)设函数f(x)=a·(b＋c)，其中向量a=(sinx，－cosx)，b=(sinx，－3cosx)，c=(－cos x，sin x)，．

(1)求函数f(x)的最大值和最小正周期；

(2)将函数y=f(x)的图象按向量d平移，使平移后得到的图象关于坐标原点成中心对称，求长度最小的d．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网