题目内容
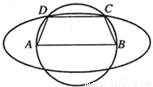
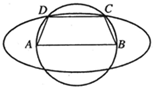 如图,已知AB=2c(常数c>0),以AB为直径的圆有一内接梯形ABCD,且AB∥CD,若椭圆以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最大时,椭圆的离心率为
如图,已知AB=2c(常数c>0),以AB为直径的圆有一内接梯形ABCD,且AB∥CD,若椭圆以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最大时,椭圆的离心率为| 3 |
| 3 |
分析:设∠BAC=θ,作CE⊥AB于点E,则可表示出BC,EB,CD,进而可求得梯形的周长的表达式,根据二次函数的性质求得周长的最大值时θ的值,则AC和BC可求,进而根据椭圆的定义求得椭圆的长轴,利用离心率公式,可得结论.
解答: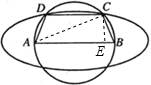 解:设∠BAC=θ,过C作CE⊥AB,垂足为E,则
解:设∠BAC=θ,过C作CE⊥AB,垂足为E,则
BC=2csinθ,EB=BCcos(90°-θ)=2csin2θ,∴CD=2c-4csin2θ,
梯形的周长l=AB+2BC+CD=2c+4csinθ+2c-4csin2=-4c(sinθ-
)2+5c.
当sinθ=
,即θ=30°时,l有最大值5c,这时,BC=c,AC=
c,a=
(AC+BC)=
c,
∴e=
=
=
-1.
故答案
-1
 解:设∠BAC=θ,过C作CE⊥AB,垂足为E,则
解:设∠BAC=θ,过C作CE⊥AB,垂足为E,则BC=2csinθ,EB=BCcos(90°-θ)=2csin2θ,∴CD=2c-4csin2θ,
梯形的周长l=AB+2BC+CD=2c+4csinθ+2c-4csin2=-4c(sinθ-
| 1 |
| 2 |
当sinθ=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∴e=
| c |
| a |
| c | ||||
|
| 3 |
故答案
| 3 |
点评:本题主要考查了椭圆的应用,考查椭圆与圆的综合,考查椭圆的几何性质,属于中档题.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 如图,已知
如图,已知 (2011•孝感模拟)如图,已知长度为2的线段AB的两个端点在动圆O的圆周上运动,O为圆心,则
(2011•孝感模拟)如图,已知长度为2的线段AB的两个端点在动圆O的圆周上运动,O为圆心,则 如图,已知
如图,已知