题目内容
如图所示,公园里有一块边长为2a的正三角形草坪,图中DE把草坪分成等面积的两部分,D在AB上,E在AC上.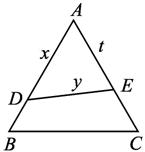
(1)设AD=x,ED=y,求y关于x的函数关系式.
(2)如果DE是灌溉水管,为节约成本,希望它最短,那么DE的位置应设在哪里?如果DE是参观路线,则希望它最长,DE的位置又应设在哪里?请予以证明.
分析:必须先用x的代数式表示AE,以下才有条件用x的代数式表示y.
解:(1)设AE=t,∵S△ADE=![]() S△ABC,
S△ABC,
即![]() txsinA=
txsinA=![]() ·
·![]() (2a)2sinA,∴tx=2a2,t=
(2a)2sinA,∴tx=2a2,t=![]() .
.
由余弦定理:y2=x2+t2-2txcosA,即y2=x2+![]() -2a2.
-2a2.
∵y>0,∴所求y与x的函数关系式为y=![]() (0<x≤2a).
(0<x≤2a).
(2)y与y2有相同的单调性,且(y2)′=2x-![]() ,
,
令(y2)′=0,则2x4-8a4=0,得x=![]() a.
a.
当x∈(0,![]() a]时,(y2)′≤0;
a]时,(y2)′≤0;
当x∈[2a,![]() a]时,(y2)′≥0.
a]时,(y2)′≥0.
∴y2在(0,![]() a]上单调递减而在[
a]上单调递减而在[![]() a,2a]上单调递增.
a,2a]上单调递增.
故当x=![]() a时,ymin=
a时,ymin=![]() a,当x=2a时,ymax=
a,当x=2a时,ymax=![]() a.
a.
答:为使DE最短,应使AD=![]() a(此时△ADE为正三角形);为使DE最长,应使AD=2a(即D与B重合,此时E为AC中点).
a(此时△ADE为正三角形);为使DE最长,应使AD=2a(即D与B重合,此时E为AC中点).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目