题目内容
(本小题共9分)
已知函数f(x)=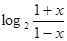 。
。
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)判断函数f(x)的奇偶性,并证明;
(Ⅲ)判断函数f(x)在定义域上的单调性,并用定义证明。
【答案】
(1)x∈(-1,1)(2)奇函数(3)根据函数的定义法加以证明,一设二作差,三变形,四定号来完成,并下结论,属于基础题。
【解析】
试题分析:解:(Ⅰ)由 >0,解得-1<x<1,所以f(x)的定义域是(-1,1) 3分
>0,解得-1<x<1,所以f(x)的定义域是(-1,1) 3分
证明:(Ⅱ)由(Ⅰ)知x∈(-1,1)
又因为f(-x)= 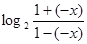 =
= =
=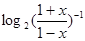 =-
=- =-f(x).
=-f(x).
所以函数f(x)是奇函数。 6分
(Ⅲ)设-1<x<x<1,
f(x)-f(x)= -
-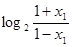 =
=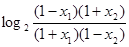
因为1-x>1-x>0;1+ x>1+ x>0,
所以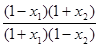 >1. 所以
>1. 所以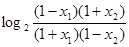 >0.
>0.
所以函数f(x)=  在(-1,1)上是增函数.
9分
在(-1,1)上是增函数.
9分
考点:函数概念和性质的运用
点评:解决该试题的关键是能利用函数的性质来分析证明函数单调性以及奇偶性的判定,属于基础题。

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 人,成绩只有
人,成绩只有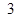 、
、 、
、 三种分值,设
三种分值,设 分别表示项目A与项目B成绩.例如:表中项目A成绩为
分别表示项目A与项目B成绩.例如:表中项目A成绩为 且
且 的概率是
的概率是 .
.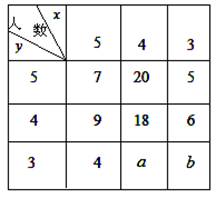
 名礼仪小姐,则
名礼仪小姐,则 的礼仪小姐中应抽多少人?
的礼仪小姐中应抽多少人? ,
, ,项目B为3分的礼仪小姐中,求项目A得3分的人数比得4分人数多的概率.
,项目B为3分的礼仪小姐中,求项目A得3分的人数比得4分人数多的概率. x+
x+ )(x∈R,
)(x∈R, )的部分图象如图所示。
)的部分图象如图所示。
 )的单调递增区间。
)的单调递增区间。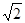 sin(2x+
sin(2x+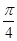 ),x∈R.
),x∈R. A)∩B;
A)∩B;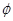 ,求a的取值范围。
,求a的取值范围。