题目内容
已知数列{an}的前n项和为Sn,数列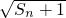 是公比为2的等比数列.
是公比为2的等比数列.
(1)证明:数列{an}成等比数列的充要条件是a1=3;
(2)设bn=5n-(-1)nan(n∈N*).若bn<bn+1对n∈N*恒成立,求a1的取值范围.
解:(1)因为数列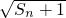 是公比为2的等比数列,
是公比为2的等比数列,
所以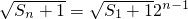 ,
,
即Sn+1=(a1+1)•4n-1.
因为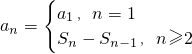 所以
所以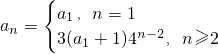
显然,当n≥2时,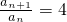 .
.
①充分性:当a1=3时,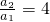 ,所以对n∈N*,都有
,所以对n∈N*,都有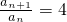 ,即数列{an}是等比数列.
,即数列{an}是等比数列.
②必要性:因为{an}是等比数列,所以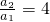 ,即
,即 ,解得a1=3.
,解得a1=3.
(2)当n=1时,b1=5+a1;当n≥2时,bn=5n-(-1)n×3(a1+1)×4n-2(a1>-1).
①当n为偶数时,5n-3(a1+1)×4n-2<5n+1+3(a1+1)×4n-1恒成立.
即15(a1+1)×4n-2>-4×5n恒成立.故a1∈(-1,+∞).
②当n为奇数时,b1<b2且bn<bn+1(n≥3)恒成立.
由b1<b2知,5+a1<25-3(a1+1),得 .
.
由bn<bn+1对n≥3的奇数恒成立,知5n+3(a1+1)×4n-2<5n+1-3(a1+1)×4n-1恒成立,
即15(a1+1)×4n-2<4×5n恒成立,所以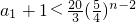 恒成立.
恒成立.
因为当对n≥3的奇数时,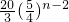 的最小值为
的最小值为 ,所以
,所以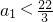 .
.
又因为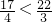 ,故
,故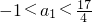 .
.
综上所述,bn<bn+1对n∈N*恒成立时, .
.
分析:(1)由题设知Sn+1=(a1+1)•4n-1.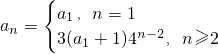 .先证明充分性:当a1=3时,
.先证明充分性:当a1=3时,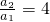 ,所以对n∈N*,都有
,所以对n∈N*,都有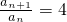 ,即数列{an}是等比数列.再证明必要性:因为{an}是等比数列,所以
,即数列{an}是等比数列.再证明必要性:因为{an}是等比数列,所以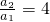 ,即
,即 ,解得a1=3.
,解得a1=3.
(2)当n=1时,b1=5+a1;当n≥2时,bn=5n-(-1)n×3(a1+1)×4n-2(a1>-1).当n为偶数时,15(a1+1)×4n-2>-4×5n恒成立.故a1∈(-1,+∞).当n为奇数时,b1<b2且bn<bn+1(n≥3)恒成立.5+a1<25-3(a1+1),得 .由此入手能够得到a1的取值范围.
.由此入手能够得到a1的取值范围.
点评:本题考查等比数列的性质,解题时感受知识点的有效组合,注意积累解题方法.
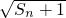 是公比为2的等比数列,
是公比为2的等比数列,所以
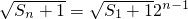 ,
,即Sn+1=(a1+1)•4n-1.
因为
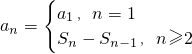 所以
所以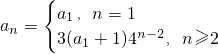
显然,当n≥2时,
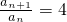 .
.①充分性:当a1=3时,
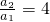 ,所以对n∈N*,都有
,所以对n∈N*,都有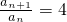 ,即数列{an}是等比数列.
,即数列{an}是等比数列.②必要性:因为{an}是等比数列,所以
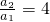 ,即
,即 ,解得a1=3.
,解得a1=3.(2)当n=1时,b1=5+a1;当n≥2时,bn=5n-(-1)n×3(a1+1)×4n-2(a1>-1).
①当n为偶数时,5n-3(a1+1)×4n-2<5n+1+3(a1+1)×4n-1恒成立.
即15(a1+1)×4n-2>-4×5n恒成立.故a1∈(-1,+∞).
②当n为奇数时,b1<b2且bn<bn+1(n≥3)恒成立.
由b1<b2知,5+a1<25-3(a1+1),得
 .
.由bn<bn+1对n≥3的奇数恒成立,知5n+3(a1+1)×4n-2<5n+1-3(a1+1)×4n-1恒成立,
即15(a1+1)×4n-2<4×5n恒成立,所以
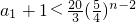 恒成立.
恒成立.因为当对n≥3的奇数时,
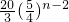 的最小值为
的最小值为 ,所以
,所以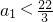 .
.又因为
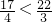 ,故
,故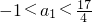 .
.综上所述,bn<bn+1对n∈N*恒成立时,
 .
.分析:(1)由题设知Sn+1=(a1+1)•4n-1.
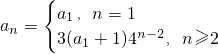 .先证明充分性:当a1=3时,
.先证明充分性:当a1=3时,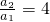 ,所以对n∈N*,都有
,所以对n∈N*,都有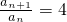 ,即数列{an}是等比数列.再证明必要性:因为{an}是等比数列,所以
,即数列{an}是等比数列.再证明必要性:因为{an}是等比数列,所以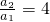 ,即
,即 ,解得a1=3.
,解得a1=3.(2)当n=1时,b1=5+a1;当n≥2时,bn=5n-(-1)n×3(a1+1)×4n-2(a1>-1).当n为偶数时,15(a1+1)×4n-2>-4×5n恒成立.故a1∈(-1,+∞).当n为奇数时,b1<b2且bn<bn+1(n≥3)恒成立.5+a1<25-3(a1+1),得
 .由此入手能够得到a1的取值范围.
.由此入手能够得到a1的取值范围.点评:本题考查等比数列的性质,解题时感受知识点的有效组合,注意积累解题方法.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |