Question

设F为抛物线y²=2px（p＞0）的焦点，点A在抛物线上，O为坐标原点，若∠OFA=120°，且

FO

•

FA

=-8，则抛物线的焦点到准线的距离等于______．

Answer 1

由y²=2px知焦点坐标为F（

p

2

，0）．
|

FO

|=

p

2

，
∵

FO

•

FA

=-8，
∴|

FO

|•|

FA

|cos∠OFA=-8，
即

p

2

•|

FA

|(-

1

2

)=-8，
∴|

FA

|=

32

p

①
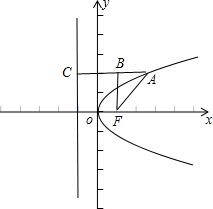
又∠BFA=∠OFA-90°=30°，
过A作准线的垂线AC，过F作AC的垂线，垂足分别为C，B．如图，
A点到准线的距离为：d=|AB|+|BC|=p+

32

p

×

1

2

，
根据抛物线的定义得：
d=|

FA

|=p +

32

p

×

1

2

②
由①②解得p=4，
则抛物线的焦点到准线的距离等于4
故答案为 4．