题目内容

已知P1（x1，y1），P2（x2，y2）是直线ax+by+c=0（b≠0）上的两点，则P1P2的长是（　　）
A、
a2+b2
|b|
|x1-x2|
B、
1
a2+b2
|x1-x2|
C、
a2+b2
|x1-x2|
D、
a2+b2
|b|
|x1+x2|
分析：用两点间距离公式消去y即可解得．
解答：解：∵P1（x1，y1），P2（x2，y2）是直线ax+by+c=0（b≠0）上的两点
∴y1=-
a
b
x1-
c
b
，y2=-
a
b
x2-
c
b

∴y1-y2=-
a
b
(x1-x2)
由两点间距离公式知，
|P1P2|=
(x1-x2)2+(y1-y2)2

=
(1-
a2
b2
)(x1-x2)2

=
a2+b2
|b|
|x1-x2|
故选A．
点评：本题主要考查直线一般式方程的应用，两点间距离公式的化简，属于基础题．
练习册系列答案
相关题目
（2006•宣武区一模）已知P1（x1，y1）是直线l：f（x，y）=0上的一点，P2（x2，y2）是直线l外的一点，由方程f（x，y）+f（x1，y1）+f（x2，y2）=0表示的直线与直线l的位置关系是（　　）
已知P1（x1，y1），P2（x2，y2）是函数f(x)=
2x
2x+
2
图象上的两点，且
OP
=
1
2
(
OP1
+
OP2
)，点P、A、B共线，且
CP
=x1
CA
+x2
CB

（1）求P点坐标
（2）若S2011=
2010
i=1
f(
i
2011
)，求S2011
（3）若Sn=
n
i=1
f(
i
n
)，记Tn为数列{
1
(Sn+
2
)(Sn+1+
2
)
}前n项的和，若Tn＜a(Sn+1+
2
)时，对一切n∈N*都成立，试求a的取值范围．
已知P1（x1，y1）、P2（x2，y2）是抛物线y2=2Px（P＞0）上两个不同点，则y1·y2=-P2是直线P1P2过焦点的（    ）

A.充分不必要条件                     B.必要不充分条件

C.充要条件                              D.既不充分也不必要条件
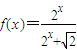已知P1（x1，y1），P2（x2，y2）是函数图象上的两点，且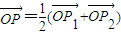，点P、A、B共线，且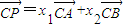
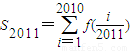（1）求P点坐标
（2）若，求S2011
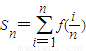（3）若，记Tn为数列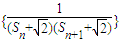前n项的和，若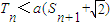时，对一切n∈N*都成立，试求a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网