题目内容
已知双曲线c: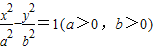 的一个焦点与抛物线y2=4x的焦点重合,且双曲线的离心率为
的一个焦点与抛物线y2=4x的焦点重合,且双曲线的离心率为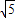 .
.(1)求双曲线的方程;
(2)若有两个半径相同的圆c1,c2,它们的圆心都在x轴上方且分别在双曲线c的两渐近线上,过双曲线的右焦点且斜率为-1的直线l与圆c1,c2都相切,求两圆c1,c2圆心连线斜率的范围.
【答案】分析:(1)由抛物线y2=4x得焦点(1,0),得双曲线的c=1.再利用离心率计算公式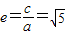 ,及a2+b2=c2,即可解得a,b;
,及a2+b2=c2,即可解得a,b;
(2)利用点斜式得直线l的方程为x+y-1=0.由(1)可得双曲线的渐近线方程为y=±2x.进而可设圆c1:(x-t)2+(y-2t)2=r2,圆c2:(x-n)2+(y+2n)2=r2,其中t>0,n<0.
因为直线l与圆c1,c2都相切,利用点到直线的距离公式可得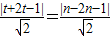 ,经过化简可得n与t的关系,再利用斜率计算公式即可得出k=
,经过化简可得n与t的关系,再利用斜率计算公式即可得出k=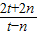 ,把n与t的关系代入即可得出k的取值方法.
,把n与t的关系代入即可得出k的取值方法.
解答:解:(1)由抛物线y2=4x得焦点(1,0),得双曲线的c=1.
又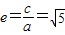 ,a2+b2=c2,
,a2+b2=c2,
解得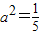 ,
,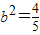 .
.
∴双曲线的方程为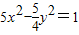 .
.
(2)直线l的方程为x+y-1=0.
由(1)可得双曲线的渐近线方程为y=±2x.
由已知可设圆c1:(x-t)2+(y-2t)2=r2,圆c2:(x-n)2+(y+2n)2=r2,其中t>0,n<0.
因为直线l与圆c1,c2都相切,所以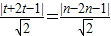 ,
,
得直线l与t+2t-1=n-2n-1,或t+2t-1=-n+2n+1,即n=-3t,或n=3t-2,
设两圆c1,c2圆心连线斜率为k,则k= ,当n=-3t时,
,当n=-3t时,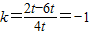 ;
;
当n=3t-2时,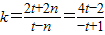 ,
,
∵t>0,n<0,∴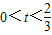 ,故可得-2<k<2,
,故可得-2<k<2,
综上:两圆c1,c2圆心连线斜率的范围为(-2,2).
点评:本题综合考查了双曲线的标准方程及其性质、直线与圆相切、点到直线的距离公式、斜率计算公式等基础知识与基本技能,考查了推理能力和计算能力.
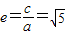 ,及a2+b2=c2,即可解得a,b;
,及a2+b2=c2,即可解得a,b;(2)利用点斜式得直线l的方程为x+y-1=0.由(1)可得双曲线的渐近线方程为y=±2x.进而可设圆c1:(x-t)2+(y-2t)2=r2,圆c2:(x-n)2+(y+2n)2=r2,其中t>0,n<0.
因为直线l与圆c1,c2都相切,利用点到直线的距离公式可得
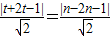 ,经过化简可得n与t的关系,再利用斜率计算公式即可得出k=
,经过化简可得n与t的关系,再利用斜率计算公式即可得出k=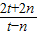 ,把n与t的关系代入即可得出k的取值方法.
,把n与t的关系代入即可得出k的取值方法.解答:解:(1)由抛物线y2=4x得焦点(1,0),得双曲线的c=1.
又
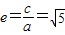 ,a2+b2=c2,
,a2+b2=c2,解得
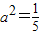 ,
,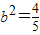 .
.∴双曲线的方程为
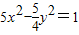 .
.(2)直线l的方程为x+y-1=0.
由(1)可得双曲线的渐近线方程为y=±2x.
由已知可设圆c1:(x-t)2+(y-2t)2=r2,圆c2:(x-n)2+(y+2n)2=r2,其中t>0,n<0.
因为直线l与圆c1,c2都相切,所以
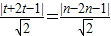 ,
,得直线l与t+2t-1=n-2n-1,或t+2t-1=-n+2n+1,即n=-3t,或n=3t-2,
设两圆c1,c2圆心连线斜率为k,则k=
 ,当n=-3t时,
,当n=-3t时,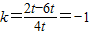 ;
;当n=3t-2时,
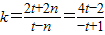 ,
,∵t>0,n<0,∴
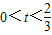 ,故可得-2<k<2,
,故可得-2<k<2,综上:两圆c1,c2圆心连线斜率的范围为(-2,2).
点评:本题综合考查了双曲线的标准方程及其性质、直线与圆相切、点到直线的距离公式、斜率计算公式等基础知识与基本技能,考查了推理能力和计算能力.

练习册系列答案
相关题目
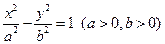 的一个焦点是
的一个焦点是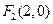 ,且
,且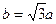 。
。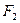 的直线
的直线 的一个法向量为
的一个法向量为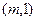 ,当直线
,当直线
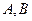 不同的两点时,求实数
不同的两点时,求实数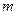 的取值范围;并证明
的取值范围;并证明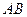 中点
中点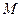 在曲线
在曲线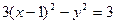 上。
上。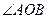 为锐角?若存在,请求出
为锐角?若存在,请求出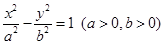 的一个焦点是
的一个焦点是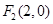 ,且
,且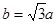 。
。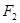 的直线
的直线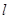 的一个法向量为
的一个法向量为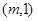 ,当直线
,当直线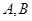 不同的两点时,求实数
不同的两点时,求实数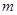 的取值范围;并证明
的取值范围;并证明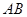 中点
中点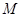 在曲线
在曲线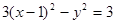 上。
上。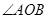 为锐角?若存在,请求出
为锐角?若存在,请求出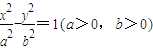 的一个焦点是F2(2,0),且
的一个焦点是F2(2,0),且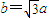 .
.