题目内容
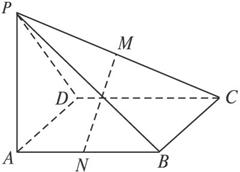
如图,M、N是直角梯形PABC两腰的中点,∠BAP=90°,CD⊥PA于D,且AB=AD.现将△PDC沿DC折起,使二面角PDCA为45°,且点P在平面ABCD内的射影恰为点A,在折起后的图形中: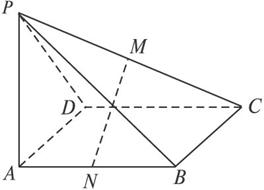
(1)求证:MN⊥面PDC;
(2)求二面角B-PC-A的大小.
(1)证明:折叠后的图形如图所示.

由题可知,PA⊥面ABCD且∠PDA=45°.
取PD中点E,连接ME、AE,

∵PA⊥面ABCD,∴PA⊥CD.又∵CD⊥AD,∴CD⊥面PAD.∴CD⊥AE.
又∵∠PDA=45°,E为PD中点,PA⊥AD,∴PD⊥AE.∴AE⊥面PDC.
又∵ME∥CD∥AN,且ME=AN,∴MN∥AE.∴MN⊥面PDC.
(2)解:∵PA⊥面ABCD,

∴面PAC⊥面ABCD.过B作BO⊥AC于O,BF⊥PC于F,连接FO,∴BO⊥面PAC.
由三垂线定理的逆定理可得∠BFO为二面角BPCA的平面角,
设AB=a,可得BO=![]() a,同(1)可证CB⊥面PAB,
a,同(1)可证CB⊥面PAB,
∴CB⊥PB.可求BF=![]() a,∴sin∠BFO=
a,∴sin∠BFO=![]() .
.
∴二面角B-PC-A的大小为60°.

练习册系列答案
相关题目
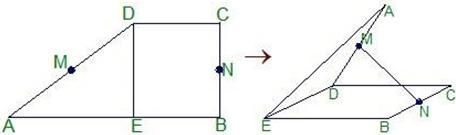
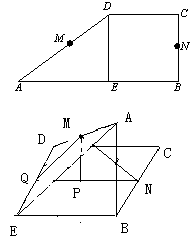
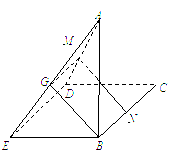 设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E (如图). 现将
设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E (如图). 现将