题目内容
6个大小相同的小球分别标有数字1,1,1,2,2,2,把它们放在一个盒子里,从中任意摸出两个小球,它们所标有的数字分别为m,n,记S=m+n.
(I)设“S=2”为事件A,求事件A发生的概率;
(II)记Smax为S的最大值,Smin为S的最小值,若a∈[0,Smax],b∈[Smin,3],设“x2+2ax+b2≥0恒成立”为事件B,求事件B发生的概率.
解:(I)由题知随机变量S的可能取值为2,3,4.
从盒子中摸出两个小球的基本事件总数为C62=15;
当S=2时,摸出的小球所标的数字为1,1,共有C32种,
∴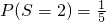
∴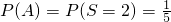
(II)试验的全部结果所构成的区域为{(a,b)|0≤a≤4,2≤b≤3};
所构成事件B的区域为{(a,b)|0≤a≤4,2≤b≤3,|a|≤|b|};
所构成事件B的概率为P(B)=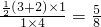 .
.
分析:(1)由题意知本题是一个古典概型,随机变量S的可能取值为2,3,4.从盒子中摸出两个小球的基本事件总数为C62,当S=2时,摸出的小球所标的数字为1,1,共有C32种.
(2)由题意知本题是一个几何概型,试验的全部结果所构成的区域为{(a,b)|0≤a≤4,2≤b≤3};所构成事件B的区域为{(a,b)|0≤a≤4,2≤b≤3,|a|≤|b|},根据几何概型公式得到结果.
点评:本小题主要考查概率、统计等基础知识,考查数据处理能力、推理论证能力、运算求解能力,以及运用数学知识分析和解决实际问题的能力.
从盒子中摸出两个小球的基本事件总数为C62=15;
当S=2时,摸出的小球所标的数字为1,1,共有C32种,
∴
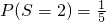
∴
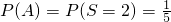
(II)试验的全部结果所构成的区域为{(a,b)|0≤a≤4,2≤b≤3};
所构成事件B的区域为{(a,b)|0≤a≤4,2≤b≤3,|a|≤|b|};
所构成事件B的概率为P(B)=
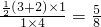 .
.分析:(1)由题意知本题是一个古典概型,随机变量S的可能取值为2,3,4.从盒子中摸出两个小球的基本事件总数为C62,当S=2时,摸出的小球所标的数字为1,1,共有C32种.
(2)由题意知本题是一个几何概型,试验的全部结果所构成的区域为{(a,b)|0≤a≤4,2≤b≤3};所构成事件B的区域为{(a,b)|0≤a≤4,2≤b≤3,|a|≤|b|},根据几何概型公式得到结果.
点评:本小题主要考查概率、统计等基础知识,考查数据处理能力、推理论证能力、运算求解能力,以及运用数学知识分析和解决实际问题的能力.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 ,求
,求 ,求
,求 ,求红球的个数;
,求红球的个数; ,求红球的个数.
,求红球的个数.