题目内容
在边长为 的正三角形ABC中,设
的正三角形ABC中,设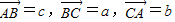 ,则a•b+b•c+c•a= .
,则a•b+b•c+c•a= .
【答案】分析:错误:a•b+b•c+c•a,应该是 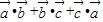
由题意可得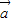 与
与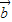 的夹角等于
的夹角等于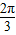 ,且|
,且|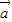 |=|
|=|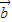 |=
|=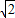 ,由此求得
,由此求得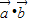 =-1,同理求得
=-1,同理求得  =
=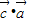 =-1,从而得到要求式子的值.
=-1,从而得到要求式子的值.
解答:解:由题意可得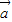 与
与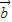 的夹角等于
的夹角等于 ,且|
,且|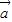 |=|
|=|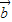 |=
|=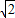 ,故有
,故有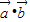 =
=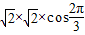 =-1.
=-1.
同理求得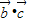 =
=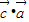 =-1,
=-1,
故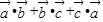 =-3,
=-3,
故答案为-3.
点评:本题主要考查两个向量的数量积的定义,注意两个向量的夹角为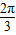 ,而不是
,而不是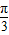 ,属于中档题.
,属于中档题.
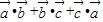
由题意可得
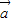 与
与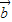 的夹角等于
的夹角等于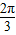 ,且|
,且|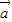 |=|
|=|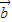 |=
|=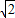 ,由此求得
,由此求得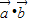 =-1,同理求得
=-1,同理求得  =
=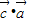 =-1,从而得到要求式子的值.
=-1,从而得到要求式子的值.解答:解:由题意可得
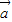 与
与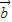 的夹角等于
的夹角等于 ,且|
,且|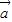 |=|
|=|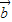 |=
|=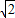 ,故有
,故有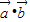 =
=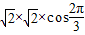 =-1.
=-1.同理求得
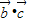 =
=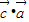 =-1,
=-1,故
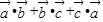 =-3,
=-3,故答案为-3.
点评:本题主要考查两个向量的数量积的定义,注意两个向量的夹角为
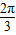 ,而不是
,而不是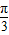 ,属于中档题.
,属于中档题. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的正三角形ABC中,设
的正三角形ABC中,设 ,则
,则 等于( )
等于( )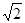 的正三角形ABC中,设
的正三角形ABC中,设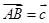 ,
, 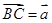 ,
, 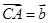 .则
.则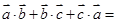 ( )
( )