题目内容

在三棱锥S-ABC中，若底面ABC是边长等于2
3
的正三角形，SA与底面ABC垂直，SA=6，点M，N分别为SB，AC的中点，则异面直线MN与BC所成角的大小为
60°
60°
．
分析：取AB的中点D，连结MD，DN，则DN∥BC，所以MN与DN所成的角即为异面直线MN与BC所成角，然后根据边角关系进行求解即可．
解答：解：取AB的中点D，连结MD，DN，因为M，N分别为SB，AC的中点，所以DN为三角形ABC的中位线，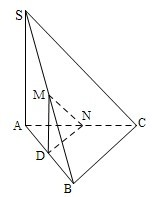
所以DN∥BC，且DN=
1
2
BC=
1
2
×2
3
=
3
，所以MN与DN所成的角即为异面直线MN与BC所成角，
因为SA与底面ABC垂直，所以DM∥SA，所以DM⊥ABC，
即DM⊥DN，所以三角形MDN为直角三角形．
因为DM=
1
2
SA=
1
2
×6=3，所以在直角三角形MDN中，
tanMDN=
DM
DN
=
3
3
=
3
，所以∠MDN=60°，
故异面直线MN与BC所成角的大小为60°
故答案为：60°
点评：本题主要考查异面直线所成角的求法，利用平行直线将异面直线转化为共面直线的夹角是解决异面直线所成角的常用方法．
练习册系列答案
相关题目
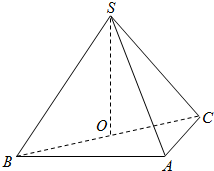精英家教网如图，在三棱锥S-ABC中，侧面SAB与侧面SAC均为边长为1的等边三角形，∠BAC=90°，O为BC中点．
（Ⅰ）证明：SO⊥平面ABC；
（Ⅱ）证明：SA⊥BC；
（Ⅲ）求三棱锥S-ABC的体积．
精英家教网如图，在三棱锥S-ABC中，侧面SAB与侧面SAC均为等边三角形，∠BAC=90°，O为BC中点．
（Ⅰ）证明：SO⊥平面ABC；
（Ⅱ）求二面角A-SC-B的余弦值．
精英家教网如图，在三棱锥S-ABC中，侧面SAB⊥底面ABC，且∠ASB=∠ABC=90°，AS=SB=2，AC=2
3
．

（Ⅰ）求证SA⊥SC；
（Ⅱ）在平面几何中，推导三角形内切圆的半径公式r=
2S
l
（其中l是三角形的周长，S是三角形的面积），常用如下方法（如右图）：
①以内切圆的圆心O为顶点，将三角形ABC分割成三个小三角形：△OAB，△OAC，△OB精英家教网C．
②设△ABC三边长分别为a，b，c．由S△ABC=S△OBC+S△OAC+S△OAB，
得S=
1
2
ar+
1
2
br+
1
2
cr=
1
2
lr，则r=
2S
l
．
类比上述方法，请给出四面体内切球半径的计算公式（不要求说明类比过程），并利用该公式求出三棱锥S-ABC内切球的半径．
如图，在三棱锥S-ABC中，SA=AB=BC=AC=
2
SB=
2
SC，O为BC中点．
（1）求证：SO⊥平面ABC
（2）在线段AB上是否存在一点E，使二面角B-SC-E的平面角的余弦值为
15
5
？若存在，确定E点位置；若不存在，说明理由．
在三棱锥S-ABC中，侧棱SC⊥平面SAB，SA⊥BC，侧面△SAB，△SBC，△SAC的面积分别为1，
3
2
，3，则此三棱锥的外接球的表面积为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网