题目内容
设a,b,c依次是方程log
x+2=x,log2(x+2)=
,2x+x-2=0的根,则a,b,c的大小关系是( )
| 1 |
| 2 |
| -x |
分析:由方程log
x+2=x,化为log2x=2-x.2x+x-2=0化为2x=2-x.在同一直角坐标系中,画出函数y=log2x,y=2x,y=2-x的图象.
由图象可得a与c的大小关系.由log2(x+2)=
,可得-x≥0,可得x≤0.即b≤0,进而得出大小关系.
| 1 |
| 2 |
由图象可得a与c的大小关系.由log2(x+2)=
| -x |
解答:解:由方程log
x+2=x,化为log2x=2-x.2x+x-2=0化为2x=2-x.
在同一直角坐标系中,画出函数y=log2x,y=2x,y=2-x的图象.
由图象可得0<a<1<c.
由log2(x+2)=
,可得-x≥0,∴x≤0.∴b≤0,
综上可得:c>a>b.
故选C.
| 1 |
| 2 |

在同一直角坐标系中,画出函数y=log2x,y=2x,y=2-x的图象.
由图象可得0<a<1<c.
由log2(x+2)=
| -x |
综上可得:c>a>b.
故选C.
点评:本题考查了指数函数、对数函数的图象与性质及幂函数的单调性,属于难题.

练习册系列答案
相关题目
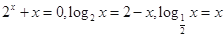 的根,则( )
的根,则( ) B.
B.  C.
C.
 D.
D.

 x=x的根,则
x=x的根,则 x=x的根,则( )
x=x的根,则( )