题目内容
(本小题满分14分)
设函数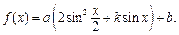
(1)当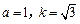 时,求函数
时,求函数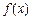 的单调减区间;
的单调减区间;
(2)当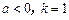 时,函数
时,函数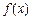 在
在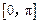 上的值域是[2,3],求a,b的值.
上的值域是[2,3],求a,b的值.
设函数
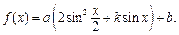
(1)当
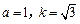 时,求函数
时,求函数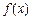 的单调减区间;
的单调减区间;(2)当
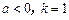 时,函数
时,函数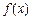 在
在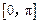 上的值域是[2,3],求a,b的值.
上的值域是[2,3],求a,b的值.(1) 函数
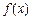 的单调减区间是
的单调减区间是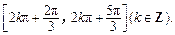
(2)
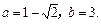
【解】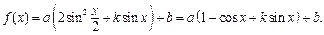 …………………2分
…………………2分
(1)当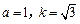 时,
时,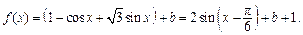 ……4分
……4分
因为函数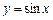 的单调减区间是
的单调减区间是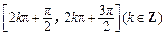 ,
,
所以当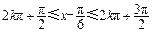 即
即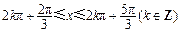 时,
时,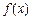 是单调减函数,
是单调减函数,
故函数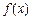 的单调减区间是
的单调减区间是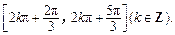 ………………………7分
………………………7分
(2)当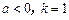 时,
时,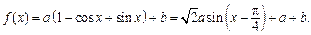 ……9分
……9分
因为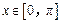 ,所以
,所以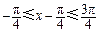 ,所以
,所以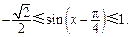
又因为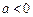 ,所以
,所以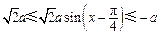 ,
,
所以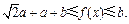 ………………………12分
………………………12分
因为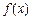 的值域是[2,3],所以
的值域是[2,3],所以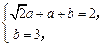
解得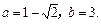 ………………………14分
………………………14分
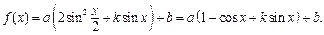 …………………2分
…………………2分(1)当
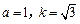 时,
时,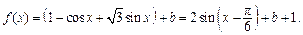 ……4分
……4分因为函数
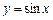 的单调减区间是
的单调减区间是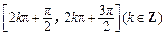 ,
,所以当
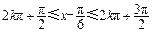 即
即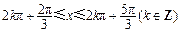 时,
时,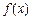 是单调减函数,
是单调减函数,故函数
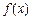 的单调减区间是
的单调减区间是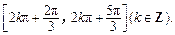 ………………………7分
………………………7分(2)当
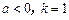 时,
时,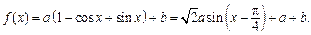 ……9分
……9分因为
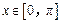 ,所以
,所以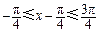 ,所以
,所以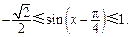
又因为
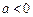 ,所以
,所以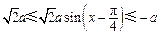 ,
,所以
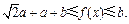 ………………………12分
………………………12分因为
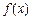 的值域是[2,3],所以
的值域是[2,3],所以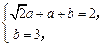
解得
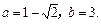 ………………………14分
………………………14分
练习册系列答案
相关题目
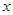 轴的非负半轴为角的始边,如果角
轴的非负半轴为角的始边,如果角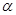 、
、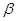 的终边分别与单位圆交于点
的终边分别与单位圆交于点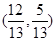 和
和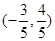 ,那么
,那么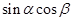 等于
等于 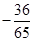
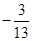
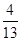
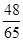
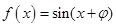 是偶函数,则
是偶函数,则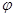 可取的一个值为( )
可取的一个值为( )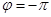
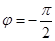
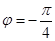
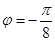
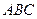 中,
中,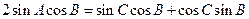 .
.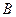 的大小;
的大小;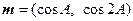 ,
,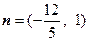 ,求当
,求当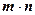 取最小值时,
取最小值时,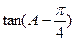 值.
值. 的图象,可以将函数
的图象,可以将函数 的图象
的图象 个单位
个单位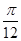 个单位
个单位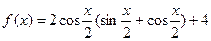 ,
,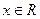 .
.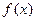 的最小正周期和单调增区间;
的最小正周期和单调增区间;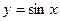
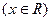 的图象经过怎样的变换得到.
的图象经过怎样的变换得到.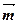 =(2sinB,2-cos2B),
=(2sinB,2-cos2B),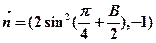 ,
,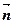 .
.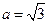 ,b=1,求c的值.
,b=1,求c的值.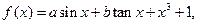 若
若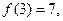 则
则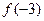 的值等于 .
的值等于 .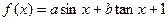 ,满足
,满足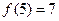 ,则
,则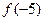 =" " ▲ .
=" " ▲ .