题目内容
若θ∈R，点P（x，y）满足方程（x-2cosθ）2+（y-2sinθ）2=1，则由点P组成的图形的面积为
8π
8π
．分析：先根据圆的标准方程求出圆心和半径，然后研究圆心的轨迹，根据点P在平面内所组成的图形是一个环面进行求解即可．
解答：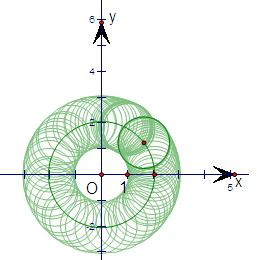
解：∵（x-2cosθ）2+（y-2sinθ）2=1的圆心为（2cosα，2sinα），半径为1，
∴圆心是以（0，0）为圆心，半径为2的圆上的动点
∴满足条件的点P在平面内所组成的图形的面积是以3为半径的圆的面积减去以1为半径的圆的面积
即9π-π=8π
故答案为：8π．
解：∵（x-2cosθ）2+（y-2sinθ）2=1的圆心为（2cosα，2sinα），半径为1，∴圆心是以（0，0）为圆心，半径为2的圆上的动点
∴满足条件的点P在平面内所组成的图形的面积是以3为半径的圆的面积减去以1为半径的圆的面积
即9π-π=8π
故答案为：8π．
点评：本题主要考查了圆的参数方程、圆方程的综合应用、圆的标准方程基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
练习册系列答案
相关题目
在A，B，C，D四小题中只能选做2题，每题10分，共计20分．