题目内容
观察下列算式:l3=1,
23=3+5,
33=7+9+11,
43=13+15+17+19,
…
若某数n3按上述规律展开后,发现等式右边含有“2013”这个数,则n= .
【答案】分析:可得规律:第n行的左边是n3,右边是n个连续奇数的和,设第n行的第一个数为an,累加可得an,计算可得a45=1981,a46=2071,可知2013在第45行.
解答:解:由题意可得第n行的左边是n3,右边是n个连续奇数的和,
设第n行的第一个数为an,则有a2-a1=3-1=2,
a3-a2=7-3=4,…an-an-1=2(n-1),
以上(n-1)个式子相加可得an-a1=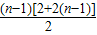 ,
,
故an=n2-n+1,可得a45=1981,a46=2071,
故可知2013在第45行,
故答案为:45
点评:本题考查类比推理,涉及累加法求数列的通项公式,属基础题.
解答:解:由题意可得第n行的左边是n3,右边是n个连续奇数的和,
设第n行的第一个数为an,则有a2-a1=3-1=2,
a3-a2=7-3=4,…an-an-1=2(n-1),
以上(n-1)个式子相加可得an-a1=
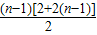 ,
,故an=n2-n+1,可得a45=1981,a46=2071,
故可知2013在第45行,
故答案为:45
点评:本题考查类比推理,涉及累加法求数列的通项公式,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目