题目内容
【题目】凸多面体的每个面均为三角形,每条棱上均标记字母![]() 之一,且每个面的三条边上恰
之一,且每个面的三条边上恰![]() 各有一个。对每一个面,当旋转多面体使该面在我们眼前时,按照字母顺序
各有一个。对每一个面,当旋转多面体使该面在我们眼前时,按照字母顺序![]() 观察其三边,若是逆时针方向,则称其为正面;否则,称其为反面。证明:正面与反面的数目之差能被4整除。
观察其三边,若是逆时针方向,则称其为正面;否则,称其为反面。证明:正面与反面的数目之差能被4整除。
【答案】见解析
【解析】
考虑标记![]() 的棱,将其中点
的棱,将其中点![]() 染红,于是,得到若干个红点.任取一条含红点的棱,有两个面以其为一条边(如图),取一个面(右),该面另两条边有一条标记
染红,于是,得到若干个红点.任取一条含红点的棱,有两个面以其为一条边(如图),取一个面(右),该面另两条边有一条标记![]() .
.
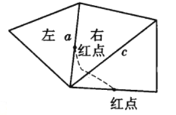
考虑以棱![]() 为边的另一个面,该面又一条棱含红点,用虚线联结这两个红点,再取另一面(左),也会有另一个红点与点
为边的另一个面,该面又一条棱含红点,用虚线联结这两个红点,再取另一面(左),也会有另一个红点与点![]() 相连.于是,任一红点均连出两条线与别的红点相连.从而,形成若干个以红点为顶点的圈.
相连.于是,任一红点均连出两条线与别的红点相连.从而,形成若干个以红点为顶点的圈.
再考虑棱![]() ,也会得到若干以蓝点(蓝点为棱
,也会得到若干以蓝点(蓝点为棱![]() 的中点)为顶点的圈.
的中点)为顶点的圈.
由于红圈、篮圈的边均要穿过一条棱![]() ,将棱
,将棱![]() 根据其被穿过的情形分为如图所示的三种类型:
根据其被穿过的情形分为如图所示的三种类型:
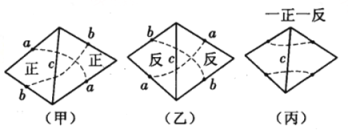
其中,图(丙)的两个红点同上或同下,连线时让它们不相交;而图中(甲)、(乙)连线时相交,且其交点不是现有的红点或蓝点.
设三种类型的数目分别为![]() .则正面数目为
.则正面数目为![]() ,反面数目为
,反面数目为![]() ,且
,且![]() 为红圈与篮圈的交点数.
为红圈与篮圈的交点数.
因为圈与圈的交点数为偶数![]() ,所以,
,所以,![]() .
.
故正面数与反面数之差能被4整除.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
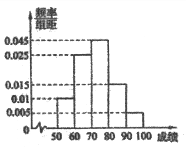
小学生10分钟应用题系列答案【题目】针对2019年“双十—”网上购物消费情况,规定:双十一当天购物消费金额不低于600元的网购者为“剁手党”,低于600元的网购者为“理智消费者”.某兴趣小组对双十一当天网购者随机抽取了100名进行抽样分析,得到如下统计图表(单位:人):
女性 | 男性 | 总计 | |
剁手党 | 50 | 5 | 55 |
理智购物者 | 30 | 15 | 45 |
总计 | 80 | 20 | 100 |
(1)根据以上统计数据回答能否在犯错误的概率不超过0.010的前提下认为“剁手党”与性别有关?
(2)现从抽取的80名女性网购者中按照分层抽样的方法选出8人,然后从选出8人中随机选出3人进行调查,选出的剁手党人数为2时的概率.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式: ,其中
,其中![]() .
.