题目内容
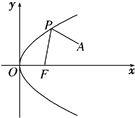 如图,F为抛物线y2=2px的焦点,A(4,2)为抛物线内一定点,P为抛物线上一动点,且|PA|+|PF|的最小值为8.
如图,F为抛物线y2=2px的焦点,A(4,2)为抛物线内一定点,P为抛物线上一动点,且|PA|+|PF|的最小值为8.(1)求该抛物线的方程;
(2)如果过F的直线l交抛物线于M、N两点,且|MN|≥32,求直线l的倾斜角的取值范围.
分析:(1)如图,设抛物线的准线为l,过P作PB⊥l于B,过A作AC⊥l于C,由抛物线定义知当且仅当A,P,C三点共线取等号.由题意知|AC|=8,从而求得p值,最后写出抛物线的方程;
(2)设直线l的方程为y=k(x-4),将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得k值的范围,从而解决问题..
(2)设直线l的方程为y=k(x-4),将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得k值的范围,从而解决问题..
解答:解:(1)设P点到抛物线的准线x=-
的距离为d,
由抛物线的定义知d=|PF|,
∴(|PA|+|PF|)min=(|PA|+d)min=
+4,
∴
+4=8⇒p=8,
∴抛物线的方程为y2=16x.…(6分)
(2)由(1)得F(4,0),设直线l的方程为y=k(x-4),显然k≠0.设M(x1,y1),N(x2,y2),
把直线方程代入抛物线,得k2x2-(8k2+16)x+16k2=0,
x1+x2=
,x1•x2=16,
∴|MN|=
×
=
×
=
×
=
×16
=
≥32,
∴k2≤1,即-1≤k≤1,
∴直线l斜率的取值范围为[-1,0)∪(0,1],
∴直线l倾斜角的取值范围为:(0,
]∪[
,π) …(13分)
| p |
| 2 |
由抛物线的定义知d=|PF|,
∴(|PA|+|PF|)min=(|PA|+d)min=
| p |
| 2 |
∴
| p |
| 2 |
∴抛物线的方程为y2=16x.…(6分)
(2)由(1)得F(4,0),设直线l的方程为y=k(x-4),显然k≠0.设M(x1,y1),N(x2,y2),
把直线方程代入抛物线,得k2x2-(8k2+16)x+16k2=0,
x1+x2=
| 8k2+16 |
| k2 |
∴|MN|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
=
| 1+k2 |
(
|
| 1+k2 |
| ||
| k2 |
=
| ||
| k2 |
| 1+k2 |
| 16(1+k2) |
| k2 |
∴k2≤1,即-1≤k≤1,
∴直线l斜率的取值范围为[-1,0)∪(0,1],
∴直线l倾斜角的取值范围为:(0,
| π |
| 4 |
| 3π |
| 4 |
点评:本题主要考查了直线与圆锥曲线的综合问题,考查了学生分析问题和解决问题的能力.当研究直线与圆锥曲线的关系的问题时,常可利用联立方程,进而利用韦达定理来解决.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
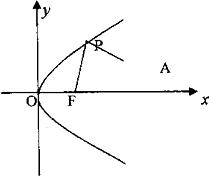
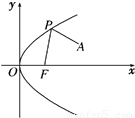 如图,F为抛物线y2=2px的焦点,A(4,2)为抛物线内一定点,P为抛物线上一动点,且|PA|+|PF|的最小值为8.
如图,F为抛物线y2=2px的焦点,A(4,2)为抛物线内一定点,P为抛物线上一动点,且|PA|+|PF|的最小值为8.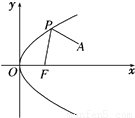 如图,F为抛物线y2=2px的焦点,A(4,2)为抛物线内一定点,P为抛物线上一动点,且|PA|+|PF|的最小值为8.
如图,F为抛物线y2=2px的焦点,A(4,2)为抛物线内一定点,P为抛物线上一动点,且|PA|+|PF|的最小值为8. 如图,F为抛物线y2=2px的焦点,A(4,2)为抛物线内一定点,P为抛物线上一动点,且|PA|+|PF|的最小值为8.
如图,F为抛物线y2=2px的焦点,A(4,2)为抛物线内一定点,P为抛物线上一动点,且|PA|+|PF|的最小值为8.