题目内容
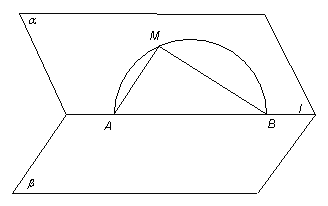
平面α内有一个半圆,直径为AB,过A作SA⊥平面α,在半圆上任取一点M,连SM、SB,且N、H分别是A在SM、SB上的射影.
(1)求证:NH⊥SB.
(2)这个图形中有多少个线面垂直关系?
(3)这个图形中有多少个直角三角形?
(4)这个图形中有多少对相互垂直的直线?
答案:
解析:
解析:
|
解:(1)连AM,BM.∵AB为已知圆的直径,如图所示.
∴AM⊥BM, ∵SA⊥平面α,MB ∴SA⊥MB. ∵AM∩SA=A,∴BM⊥平面SAM. ∵AN ∴BM⊥AN. ∵AN⊥SM于N,BM∩SM=M, ∴AN⊥平面SMB. ∵AH⊥SB于H,且NH是AH在平面SMB的射影 ∴NH⊥SB. (2)由(1)知,SA⊥平面AMB,BM⊥平面SAM.AN⊥平面SMB. ∵SB⊥AH且SB⊥HN. ∴SB⊥平面ANH. ∴图中共有4个线面垂直关系 (3)∵SA⊥平面AMB, ∴ΔSAB、ΔSAM均为直角三角形. ∵BM⊥平面SAM,∴ΔBMA,ΔBMS均为直角三角形. ∵AN⊥平面SMB.∴ΔANS、ΔANM、ΔANH均为直角三角形. ∵SB⊥平面AHN.∴ΔSHA、ΔBHA、ΔSHN均为直角三角形 综上所述,图中共有10个直角三角形. (4)由SA⊥平面AMB知:SA⊥AM,SA⊥AB,SA⊥BM; 由BM⊥平面SAM知:BM⊥AM,BM⊥SM,BM⊥AN; 由AN⊥平面SMB知:AN⊥SM,AN⊥SB,AN⊥NH; SB⊥平面AHN知:SB⊥AH,SB⊥HN; 综上所述,图中有11对互相垂直的直线. 解析:此题主要考查直线与直线,直线与平面的垂直关系及论证,空间想象力. |

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目

 如图,已知二面角α-l-β的平面角为45°,在半平面α内有一个半圆O,其直径AB在l上,M是这个半圆O上任一点(除A、B外),直线AM、BM与另一个半平面β所成的角分别为θ1、θ2.试证明cos2θ1+cos2θ2为定值.
如图,已知二面角α-l-β的平面角为45°,在半平面α内有一个半圆O,其直径AB在l上,M是这个半圆O上任一点(除A、B外),直线AM、BM与另一个半平面β所成的角分别为θ1、θ2.试证明cos2θ1+cos2θ2为定值.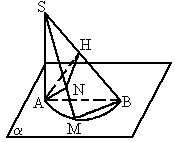

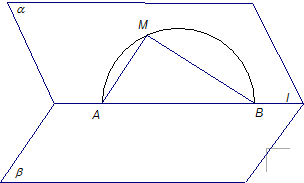 如图,已知二面角α-l-β的平面角为45°,在半平面α内有一个半圆O,其直径AB在l上,M是这个半圆O上任一点(除A、B外),直线AM、BM与另一个半平面β所成的角分别为θ1、θ2.试证明cos2θ1+cos2θ2为定值.
如图,已知二面角α-l-β的平面角为45°,在半平面α内有一个半圆O,其直径AB在l上,M是这个半圆O上任一点(除A、B外),直线AM、BM与另一个半平面β所成的角分别为θ1、θ2.试证明cos2θ1+cos2θ2为定值.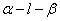 的平面角为
的平面角为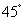 ,
在半平面
,
在半平面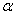 内有一个半圆
内有一个半圆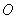 ,
其直径
,
其直径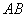 在
在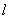 上,
上, 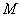 是这个半圆
是这个半圆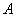 、
、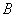 外), 直线
外), 直线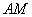 、
、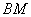 与另一个半平面
与另一个半平面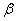 所成的角分别为
所成的角分别为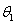 、
、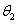 .试证明
.试证明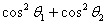 为定值.
为定值.