题目内容
(本题满分14分) 设首项为a1,公差为d的等差数列{an}的前n项和为Sn.
已知a7=-2,S5=30.
(Ⅰ) 求a1及d;
(Ⅱ) 若数列{bn}满足an=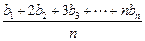 (n∈N*),
(n∈N*),
求数列{bn}的通项公式 .
.
已知a7=-2,S5=30.
(Ⅰ) 求a1及d;
(Ⅱ) 若数列{bn}满足an=
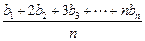 (n∈N*),
(n∈N*),求数列{bn}的通项公式
 .
.(Ⅰ)
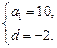
(Ⅱ) bn=
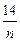 -4 (n∈N*).
-4 (n∈N*).(Ⅰ) 解:由题意可知
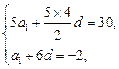 得
得
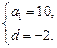 ………………………………………6分
………………………………………6分
(Ⅱ) 解:由(Ⅰ)得 an=10+(n-1)(-2)=12-2n,
所以 b1+2b2+3b3+…+nbn=nan=n(12-2n),
当n=1时,b1=10,
当n≥2时,b1+2b2+3b3+…+(n-1)bn-1=(n-1)[12-2(n-1)],
所以nbn= n(12-2n)-(n-1)[12-2(n-1)]=14-4n,
故bn=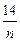 -4.
-4.
当n=1时也成立.
所以bn=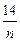 -4 (n∈N*). ……………………………14分
-4 (n∈N*). ……………………………14分
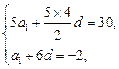 得
得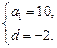 ………………………………………6分
………………………………………6分(Ⅱ) 解:由(Ⅰ)得 an=10+(n-1)(-2)=12-2n,
所以 b1+2b2+3b3+…+nbn=nan=n(12-2n),
当n=1时,b1=10,
当n≥2时,b1+2b2+3b3+…+(n-1)bn-1=(n-1)[12-2(n-1)],
所以nbn= n(12-2n)-(n-1)[12-2(n-1)]=14-4n,
故bn=
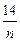 -4.
-4.当n=1时也成立.
所以bn=
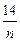 -4 (n∈N*). ……………………………14分
-4 (n∈N*). ……………………………14分
练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
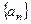 中,对一切自然数
中,对一切自然数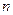 ,都有
,都有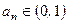 且
且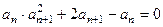 .
.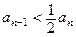 ;
;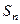 表示数列
表示数列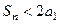 .
. 是等差数列,且
是等差数列,且
 为
为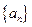 满足
满足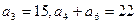 ,
,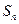 为
为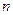 项和.
项和.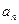 及当
及当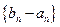 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列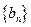 的通项公式及其前
的通项公式及其前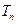 .
.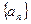 满足:
满足: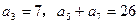 ,
,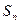 ,
,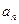 及
及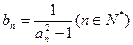 ,求数列
,求数列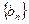 的前n项和
的前n项和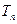 .
.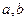 为正实数,
为正实数,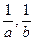 的等差中项为
的等差中项为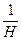 ;
;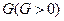 ,则( )
,则( )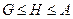 ;
;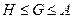 ;
;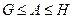 ;
;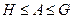 。
。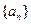 的公差为
的公差为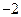 ,且
,且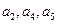 成等比数列,则
成等比数列,则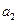 等于( )
等于( )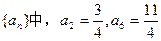
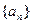 的通项公式;
的通项公式;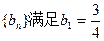 ,且
,且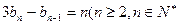 ),求证
),求证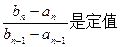 ;
;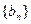 通项公式及前n项和
通项公式及前n项和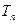 。
。