题目内容
一盒中共装有除颜色外其余均相同的小球12个,其中5个红球、4个黑球、2个白球、1个绿球.从中随机取出1个球,求:
(1)取出1球是红球或黑球的概率;
(2)取出1球是红球或黑球或白球的概率.
(1)取出1球是红球或黑球的概率;
(2)取出1球是红球或黑球或白球的概率.
(1)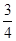 (2)
(2)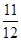
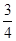 (2)
(2)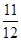
记事件A1={任取1球为红球},A2={任取1球为黑球},A3={任取1球为白球},A4={任取1球为绿球},则P(A1)=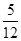 ,P(A2)=
,P(A2)=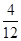 ,P(A3)=
,P(A3)=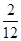 ,P(A4)=
,P(A4)=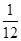 .据题意知事件A1,A2,A3,A4彼此互斥,由互斥事件的概率公式,得
.据题意知事件A1,A2,A3,A4彼此互斥,由互斥事件的概率公式,得
(1)取出1球是红球或黑球的概率为
P(A1∪A2)=P(A1)+P(A2)=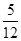 +
+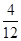 =
=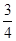 .
.
(2)取出1球是红球或黑球或白球的概率为
方法一:P(A1∪A2∪A3)=P(A1)+P(A2)+P(A3)=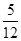 +
+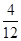 +
+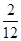 =
=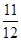 .
.
方法二:P(A1∪A2∪A3)=1-P(A4)=1-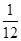 =
=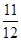 .
.
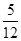 ,P(A2)=
,P(A2)=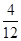 ,P(A3)=
,P(A3)=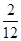 ,P(A4)=
,P(A4)=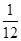 .据题意知事件A1,A2,A3,A4彼此互斥,由互斥事件的概率公式,得
.据题意知事件A1,A2,A3,A4彼此互斥,由互斥事件的概率公式,得(1)取出1球是红球或黑球的概率为
P(A1∪A2)=P(A1)+P(A2)=
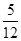 +
+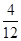 =
=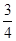 .
.(2)取出1球是红球或黑球或白球的概率为
方法一:P(A1∪A2∪A3)=P(A1)+P(A2)+P(A3)=
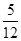 +
+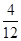 +
+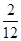 =
=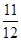 .
.方法二:P(A1∪A2∪A3)=1-P(A4)=1-
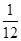 =
=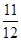 .
.
练习册系列答案
相关题目

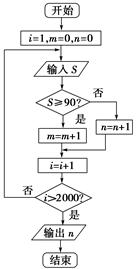
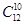 (
(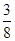 )10(
)10(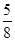 )2
)2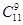 (
( 分,海选不合格记
分,海选不合格记 分.假设甲、乙、丙海选合格的概率分别为
分.假设甲、乙、丙海选合格的概率分别为 ,他们海选合格与不合格是相互独立的.
,他们海选合格与不合格是相互独立的. ,求随机变量
,求随机变量 .
.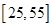 岁的人群中随机抽取n人进行了一次调查,得到如下统计表:
岁的人群中随机抽取n人进行了一次调查,得到如下统计表: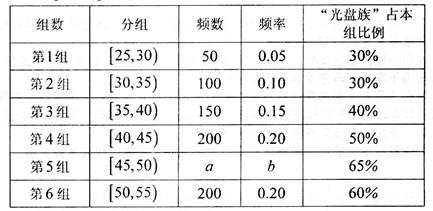
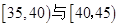 的“光盘族”中,采用分层抽样方法抽取8人参加节约粮食宣传活动,并从这8人中选取2人作为领队.
的“光盘族”中,采用分层抽样方法抽取8人参加节约粮食宣传活动,并从这8人中选取2人作为领队.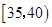 中的前提下,求另一人来自年龄段
中的前提下,求另一人来自年龄段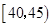 中的概率;
中的概率;