题目内容
已知函数 (x∈R)的最大值为M,最小值为m,则M+m的值为 .
(x∈R)的最大值为M,最小值为m,则M+m的值为 .
【答案】分析:由函数y=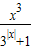 为奇函数,可得其最大值N和最小值n满足N+n=0,进而可得M=1-n,m=1-M,进而可得M+m的值.
为奇函数,可得其最大值N和最小值n满足N+n=0,进而可得M=1-n,m=1-M,进而可得M+m的值.
解答:解:函数 =1-
=1-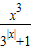
∵y=x3为奇函数,y=3|x|+1为偶函数
故函数y= 为奇函数,
为奇函数,
设函数y= 的最大值N和最小值n
的最大值N和最小值n
则N+n=0
则M=1-n,m=1-M
故M+m=(1-n)+(1-M)=2-(N+n)=2
故答案为:2
点评:本题考查的知识点是函数最值的应用,构造函数y=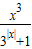 ,并分析其奇偶性,是解答的关键.
,并分析其奇偶性,是解答的关键.
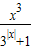 为奇函数,可得其最大值N和最小值n满足N+n=0,进而可得M=1-n,m=1-M,进而可得M+m的值.
为奇函数,可得其最大值N和最小值n满足N+n=0,进而可得M=1-n,m=1-M,进而可得M+m的值.解答:解:函数
 =1-
=1-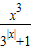
∵y=x3为奇函数,y=3|x|+1为偶函数
故函数y=
 为奇函数,
为奇函数,设函数y=
 的最大值N和最小值n
的最大值N和最小值n则N+n=0
则M=1-n,m=1-M
故M+m=(1-n)+(1-M)=2-(N+n)=2
故答案为:2
点评:本题考查的知识点是函数最值的应用,构造函数y=
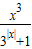 ,并分析其奇偶性,是解答的关键.
,并分析其奇偶性,是解答的关键. 
练习册系列答案
相关题目
 (x∈R)的图象为曲线C.
(x∈R)的图象为曲线C. (x∈R)的最大值为M,最小值为m,则M+m= .
(x∈R)的最大值为M,最小值为m,则M+m= . (x∈R)的图象为曲线C.
(x∈R)的图象为曲线C. (x∈R)的图象为曲线C.
(x∈R)的图象为曲线C.