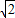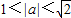题目内容
如果y=loga2-1x在(0,+∞)内是减函数,则a的取值范围是
- A.|a|>1
- B.|a|<2
- C.a<-

- D.
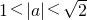
D
分析:由条件利用对数函数的单调性和特殊点可得,0<a2-1<1,由此解得a的范围.
解答:由于函数 y=loga2-1x在(0,+∞)内是减函数,∴0<a2-1<1,解得 1<a< ,或-
,或- <a<-1,
<a<-1,
即 1<|a|< ,
,
故选D.
点评:本题主要考查对数函数的单调性和特殊点,一元二次不等式的解法,属于中档题.
分析:由条件利用对数函数的单调性和特殊点可得,0<a2-1<1,由此解得a的范围.
解答:由于函数 y=loga2-1x在(0,+∞)内是减函数,∴0<a2-1<1,解得 1<a<
 ,或-
,或- <a<-1,
<a<-1,即 1<|a|<
 ,
,故选D.
点评:本题主要考查对数函数的单调性和特殊点,一元二次不等式的解法,属于中档题.

练习册系列答案
相关题目