题目内容
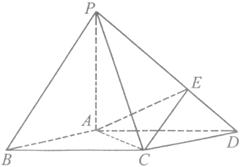
如图,在底面是菱形的四棱锥![]() 中,
中,![]() ,点E在
,点E在![]() 上,且
上,且![]()
 (I)证明:
(I)证明:![]() ;
;
(Ⅱ)求以![]() 为棱,
为棱,![]() 与
与![]() 为面
为面
的二面角![]() 的大小;
的大小;
解法一:
(I)证明:因为底面![]() 是菱形,
是菱形,![]() ,
,
所以![]() ,在
,在![]() 中,
中,
由![]() 知
知![]()
同理,![]() 所以
所以![]() 平面
平面![]()
(Ⅱ)解:作![]() 交
交![]() 于
于![]() ,
,
由![]() 平面
平面![]()
知![]() 平面
平面![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,
,
则![]() 即为二面角
即为二面角![]() 的平面角。
的平面角。
又![]() 所以
所以![]()
从而![]()
(Ⅲ)当![]() 是棱
是棱![]() 的中点时,
的中点时,![]() 平面
平面![]() 证明如下,
证明如下,
取![]() 的中点
的中点![]() ,连结
,连结![]() ,则
,则![]() ①
①
 由
由 ![]() 知
知![]() 是
是![]() 的中点
的中点
连结![]() ,设
,设![]() ,则
,则![]() 为
为![]() 的中点。
的中点。
所以 ![]() ②
②
由①、②知,平面![]() 平面
平面![]() 。
。
又 ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]()
解法二:
(I)证明:因为底面![]() 是菱形,
是菱形,![]() ,
,
所以![]() 在
在![]() 中,
中,
由![]() 知
知![]()
同理,![]() ,所以
,所以![]() 平面
平面![]()
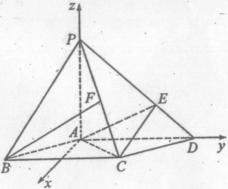
(Ⅱ)解:以A为坐标原点,直线![]() 分别为
分别为![]() 轴,
轴,![]() 轴,过
轴,过![]() 点垂直平面
点垂直平面![]() 的直线为
的直线为![]() 轴,建立空间直角坐标系如图,由题设条件,相关各点的坐标分别为
轴,建立空间直角坐标系如图,由题设条件,相关各点的坐标分别为
![]()
![]()
所以![]()
![]()
![]()
设![]() 是平面
是平面![]() 的一个法向量。
的一个法向量。
则![]()
![]() =0
=0
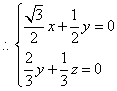 令
令![]() 得
得![]() 即
即![]()
又由已知![]() 是平面
是平面![]() 的一个法向量,且
的一个法向量,且![]()
![]() ,
, ![]()
(Ⅲ)(法一)设点![]() 是棱
是棱![]() 上的点,
上的点,![]() 其中
其中![]() ,则
,则 ![]()
![]()
由(Ⅱ)知![]() 是平面
是平面![]() 的一个法向量
的一个法向量
![]() 即
即![]()
![]() 解得
解得![]()
即![]() 是
是![]() 的中点时,
的中点时,![]() 。/
。/
又![]() 平面
平面![]() ,所以当
,所以当![]() 是棱
是棱![]() 的中点时,
的中点时,![]() 平面
平面![]()
(法二)当![]() 是棱
是棱![]() 的中点时,
的中点时,![]() 平面
平面![]() ,证明如下:
,证明如下:
因为![]()
![]()
所以 ![]() 共面。
共面。
又![]() 平面
平面![]() ,从面
,从面![]() 平面
平面![]()

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD=
如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD= 如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.
如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2. 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2