题目内容
已知函数f(x)= cos2x+sinxcosx-
cos2x+sinxcosx- ,x∈R.
,x∈R.
(I)设角a的顶点在坐标原点,始边在x轴的负半轴上,终边过点P( ,-
,- ),求f(a)的值;
),求f(a)的值;
(II)试讨论函数f(x)的基本性质(直接写出结论).
解:解法一:(I)因为点P( ,-
,- )在α终边上,
)在α终边上,
所以sin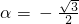 ,cos
,cos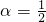
f(α)=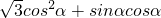 -
-
=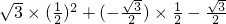 =
=
(II)f(x)= cos2x+sinxcosx-
cos2x+sinxcosx-
=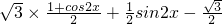
=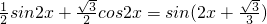
函数的基本性质如下:①函数f(x)既不是奇函数也不是偶函数;
②函数f(x)单调增区间为[kπ- ,k
,k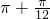 ],单调减区间为:[k
],单调减区间为:[k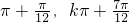 ](k∈Z);
](k∈Z);
③函数的最大值我1,最小值为-1;
④函数的周期为:π
解法二:f(x)= cos2x+sinxcosx-
cos2x+sinxcosx-
=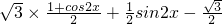
=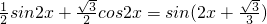
(I)因为点P( ,-
,- )在α终边上,
)在α终边上,
所以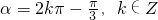
所以f(α)=sin[2(2kπ- )+
)+ ]=sin(4kπ-
]=sin(4kπ- )=sin(-
)=sin(- )=-
)=-
(II)同解法一;
分析:解法一:(I)利用点P( ,-
,- )在α终边上,求出sinα,cosα,然后求出f(α).
)在α终边上,求出sinα,cosα,然后求出f(α).
(II)化简函数的表达式为一个角的一个三角函数的形式,然后找出:奇偶性,单调性,最值,周期;
解法二:化简函数f(x)的表达式为一个角的一个三角函数的形式,
(I)点P( ,-
,- )在α终边上,求出
)在α终边上,求出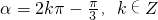 解出f(α)即可.
解出f(α)即可.
(II)同解法一;
点评:本题考查三角函数的定义、两角和与差的三角函数公式、二倍角公式、三角函数的图象与性质等知识,考查运算求解能力,转化与化归思想等.
 ,-
,- )在α终边上,
)在α终边上,所以sin
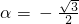 ,cos
,cos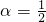
f(α)=
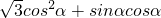 -
-
=
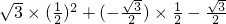 =
=
(II)f(x)=
 cos2x+sinxcosx-
cos2x+sinxcosx-
=
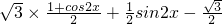
=
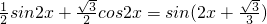
函数的基本性质如下:①函数f(x)既不是奇函数也不是偶函数;
②函数f(x)单调增区间为[kπ-
 ,k
,k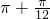 ],单调减区间为:[k
],单调减区间为:[k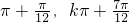 ](k∈Z);
](k∈Z);③函数的最大值我1,最小值为-1;
④函数的周期为:π
解法二:f(x)=
 cos2x+sinxcosx-
cos2x+sinxcosx-
=
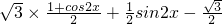
=
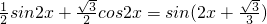
(I)因为点P(
 ,-
,- )在α终边上,
)在α终边上,所以
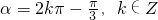
所以f(α)=sin[2(2kπ-
 )+
)+ ]=sin(4kπ-
]=sin(4kπ- )=sin(-
)=sin(- )=-
)=-
(II)同解法一;
分析:解法一:(I)利用点P(
 ,-
,- )在α终边上,求出sinα,cosα,然后求出f(α).
)在α终边上,求出sinα,cosα,然后求出f(α).(II)化简函数的表达式为一个角的一个三角函数的形式,然后找出:奇偶性,单调性,最值,周期;
解法二:化简函数f(x)的表达式为一个角的一个三角函数的形式,
(I)点P(
 ,-
,- )在α终边上,求出
)在α终边上,求出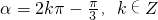 解出f(α)即可.
解出f(α)即可.(II)同解法一;
点评:本题考查三角函数的定义、两角和与差的三角函数公式、二倍角公式、三角函数的图象与性质等知识,考查运算求解能力,转化与化归思想等.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
已知函数f(x)=
,则关于x的方程f2(x)+bf(x)+c=0有5个不同实数解的充要条件是( )
|
| A、b<-2且c>0 |
| B、b>-2且c<0 |
| C、b<-2且c=0 |
| D、b≥-2且c=0 |
 已知函数f(x)的图象如图所示,则函数的值域为( )
已知函数f(x)的图象如图所示,则函数的值域为( )