题目内容
如图,已知平面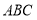
 平面
平面 ,
,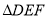 与
与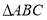 分别是棱长为1与2的正三角形,
分别是棱长为1与2的正三角形,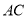 //
//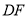 ,四边形
,四边形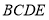 为直角梯形,
为直角梯形, //
// ,
,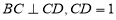 ,点
,点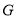 为
为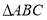 的重心,
的重心,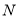 为
为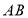 中点,
中点,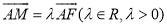 .
.

(Ⅰ)当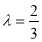 时,求证:
时,求证: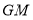 //平面
//平面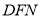 ;
;
(Ⅱ)若直线 与
与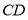 所成角为
所成角为 ,试求二面角
,试求二面角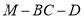 的余弦值.
的余弦值.
练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
题目内容
如图,已知平面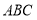
 平面
平面 ,
,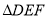 与
与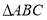 分别是棱长为1与2的正三角形,
分别是棱长为1与2的正三角形,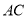 //
//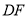 ,四边形
,四边形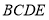 为直角梯形,
为直角梯形, //
// ,
,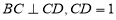 ,点
,点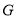 为
为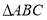 的重心,
的重心,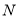 为
为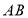 中点,
中点,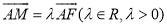 .
.

(Ⅰ)当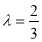 时,求证:
时,求证: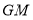 //平面
//平面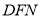 ;
;
(Ⅱ)若直线 与
与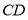 所成角为
所成角为 ,试求二面角
,试求二面角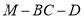 的余弦值.
的余弦值.
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案