题目内容
已知数列 满足
满足 ,
, ,数列
,数列 满足
满足 .
.
(1)求证:数列 是等差数列;
是等差数列;
(2)设 ,求满足不等式
,求满足不等式 的所有正整数
的所有正整数 的值.
的值.
 满足
满足 ,
, ,数列
,数列 满足
满足 .
.(1)求证:数列
 是等差数列;
是等差数列;(2)设
 ,求满足不等式
,求满足不等式 的所有正整数
的所有正整数 的值.
的值.(1)详见解析;(2)2,3.
试题分析:(1)要证明数列
 是等差数列,只需证明
是等差数列,只需证明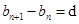 即可,而由条件中
即可,而由条件中 ,
, ,可得
,可得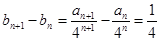 ,从而得证;(2)由(1),可以求得
,从而得证;(2)由(1),可以求得 的通项公式,结合
的通项公式,结合 ,即可求得
,即可求得 的通项公式,从而可以得到
的通项公式,从而可以得到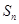 =
=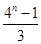 ,解关于n的不等式,即可得到满足不等式的所有整数值.
,解关于n的不等式,即可得到满足不等式的所有整数值.(1)由
 ,得
,得 ,∴
,∴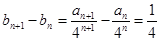 (4分)
(4分)∴数列
 是等差数列,首项
是等差数列,首项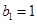 ,公差为
,公差为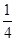 . (6分);
. (6分); (2)
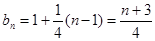 ,则
,则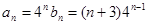 (8分)
(8分)从而有
 ,故
,故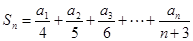
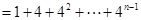
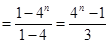 (10分)
(10分)则
 ,由
,由 ,得
,得 ,即
,即 ,得
,得 .
.故满足不等式
 的所有正整数
的所有正整数 的值为
的值为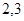 .
.
练习册系列答案
相关题目
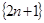 中各项划分为:(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33), (35,37,39,41)。照此下去,第100个括号里各数的和为
中各项划分为:(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33), (35,37,39,41)。照此下去,第100个括号里各数的和为  的前
的前 项和为
项和为 且
且 .
. 的前
的前 项和
项和 ,并求
,并求 的前
的前 项和为
项和为 ,已知
,已知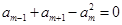 ,
, ,则
,则 ( )
( )



 成等比数列,则
成等比数列,则 也成等比数列;②若数列{
也成等比数列;②若数列{ }既是等差数列也是等比数列,则{
}既是等差数列也是等比数列,则{ ,且
,且 ,则{
,则{ ,其中正确判断的序号是______.(注:把你认为正确判断的序号都填上)
,其中正确判断的序号是______.(注:把你认为正确判断的序号都填上) 满足
满足 且
且 成等比数列,则
成等比数列,则 .
.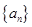 是等差数列,
是等差数列, ,
, ,则首项
,则首项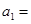 .
. 满足:
满足: ,且对任意的m,n∈N*都有:
,且对任意的m,n∈N*都有: ,则
,则 ( )
( )


