题目内容
(5分)(2011•湖北)若向量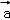 =(1,2),
=(1,2),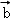 =(1,﹣1),则2
=(1,﹣1),则2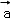 +
+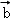 与
与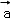
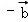 的夹角等于( )
的夹角等于( )
A.﹣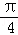 | B.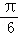 | C.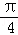 | D.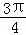 |
C
解析试题分析:由已知中向量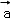 =(1,2),
=(1,2),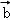 =(1,﹣1),我们可以计算出2
=(1,﹣1),我们可以计算出2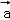 +
+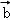 与
与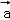
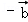 的坐标,代入向量夹角公式即可得到答案.
的坐标,代入向量夹角公式即可得到答案.
解:∵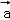 =(1,2),
=(1,2),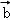 =(1,﹣1),
=(1,﹣1),
∴2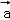 +
+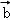 =(3,3)
=(3,3)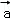
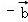 =(0,3)
=(0,3)
则(2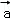 +
+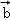 )•(
)•(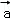
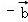 )=9
)=9
|2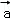
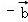 |=
|=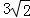 ,|
,|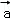
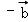 |=3
|=3
∴cosθ=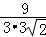 =
=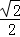
∴θ=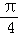
故选C
点评:本题考查的知识点是数量积表示两个向量的夹角,其中利用公式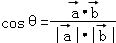 ,是利用向量求夹角的最常用的方法,一定要熟练掌握.
,是利用向量求夹角的最常用的方法,一定要熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设向量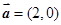 ,
,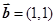 ,则下列结论中正确的是
,则下列结论中正确的是
A.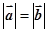 | B.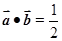 | C.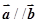 | D.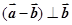 |
已知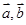 均为单位向量,它们的夹角为60°,那么
均为单位向量,它们的夹角为60°,那么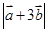 =( )
=( )
A.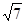 | B.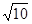 | C.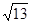 | D.4 |
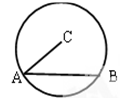
如图,半径为R的圆C中,已知弦AB的长为5,则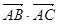 =( )
=( )
A.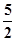 | B.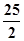 | C.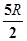 | D.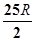 |
设向量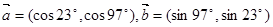 ,则
,则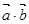 等于 ( )
等于 ( )
A.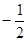 | B.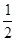 | C. | D.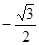 |
已知向量 ,
, 满足:
满足: ,且
,且 (
( ).则向量
).则向量 与向量
与向量 的夹角的最大值为( ).
的夹角的最大值为( ).
A. | B. | C. | D. |
[2013·重庆诊测]若向量a=(1,λ,2),b=(2,-1,2),且a与b的夹角余弦值为 ,则λ等于( )
,则λ等于( )
| A.2 | B.-2 | C.-2或 | D.2或- |
对任意两个非零的平面向量α和β,定义 .若两个非零的平面向量
.若两个非零的平面向量 和
和 ,满足
,满足 与
与 的夹角
的夹角 ,且
,且 和
和 都在集合
都在集合 中,则
中,则 =
=
A. | B. | C.1 | D. |
 -t
-t )·
)·