题目内容
已知椭圆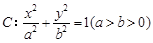
的离心率为
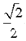,其中左焦点
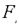(-2,0).
(1) 求椭圆C的方程;
(2) 若直线y=x+m与椭圆C交于不同的两点A,B,且线段AB的中点M在圆x2+y2=1上,求m的值.
【答案】
(1) 
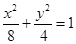;(2)
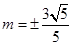
【解析】
试题分析：（1）根据椭圆的基本性质列三个关于a,b,c的方程即可求出a,b。从而求出椭圆方程。（2）联立方程组消去y得到3x2+4mx+2m2-8=0，因为有两个交点，所以判别式大于0，解出m的范围，再由韦达定理得到两根之和，两根之积。根据中点坐标公式求出中点坐标，在将其代入圆的方程即可求出m.
试题解析： (1) 由题意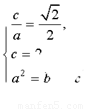,得
解得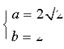
∴椭圆C的方程为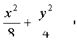
(2) 设点A、B的坐标分别为(x1,y1),(x2, y2),线段AB的中点为M(x0,y0),
由
消y得,3x2+4mx+2m2-8=0,
Δ=96-8m2>0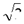,∴-2
<m<2.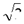
∴
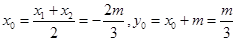
∵点M(x0,y0)在圆x2+y2=1上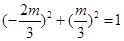,] 所以
，所以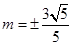
考点：椭圆方程，直线与圆锥曲线的位置关系
练习册系列答案
发散思维新课堂系列答案
相关题目
已知椭圆的离心率为e，两焦点分别为F1、F2，抛物线C以F1为顶点、F2为焦点，点P为抛物线和椭圆的一个交点，若e|PF2|=|PF1|，则e的值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
已知椭圆的离心率为
，焦点是（-3，0），（3，0），则椭圆方程为（ ）
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在由圆O：x2+y2=1和椭圆C：
如图，A，B是椭圆C：