题目内容
已知无穷数列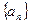 中,
中, 是首项为
是首项为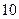 ,公差为
,公差为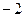 的等差数列;
的等差数列;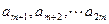 是首项为
是首项为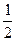 ,公比为
,公比为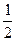 的等比数列
的等比数列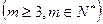 ,并对任意
,并对任意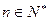 ,均有
,均有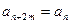 成立,(1)当
成立,(1)当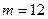 时,求
时,求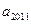 ; (2)若
; (2)若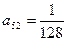 ,试求
,试求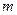 的值;(3)判断是否存在
的值;(3)判断是否存在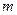 ,使
,使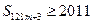 成立,若存在,求出
成立,若存在,求出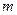 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)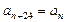 ;所以
;所以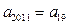 ---------2分
---------2分 是以
是以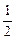 为首项,以
为首项,以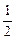 为公比的等比数列的第7项,所以
为公比的等比数列的第7项,所以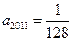 3分
3分
(2)因为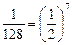 ,所以
,所以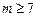 ------4分 因为
------4分 因为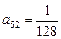 ,所以
,所以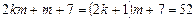 ,其中
,其中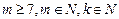
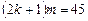 , -----------5分
, -----------5分
当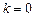 时,
时,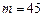 ,成立; 当
,成立; 当 时,
时,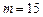 ,成立;
,成立;
当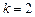 时,
时,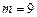 ,成立; 当
,成立; 当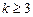 时,
时,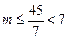 ;
;
所以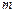 可取9、15、45 -----------6分
可取9、15、45 -----------6分
(3) 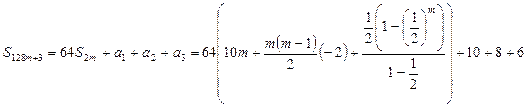
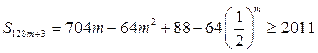
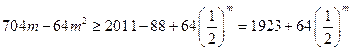
设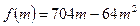 ,
,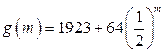 -----------10分
-----------10分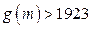 ;
; 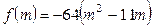 ,对称轴
,对称轴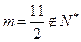 ,
,
所以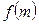 在
在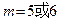 时取最大
时取最大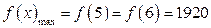
因为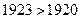 ,所以不存在这样的
,所以不存在这样的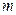 .
.
解析

练习册系列答案
相关题目
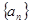 中,
中,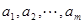 是首项为
是首项为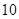 ,公差为
,公差为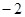 的等差数列;
的等差数列;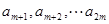 是首项为
是首项为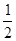 ,公比为
,公比为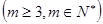 ,并对任意
,并对任意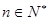 ,均有
,均有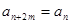 成立,(1)当
成立,(1)当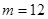 时,求
时,求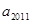 ; (2)若
; (2)若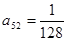 ,试求
,试求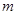 的值;(3)判断是否存在
的值;(3)判断是否存在 成立,若存在,求出
成立,若存在,求出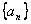 中,
中,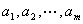 是首项为
是首项为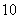 ,公差为
,公差为 的等差数列;
的等差数列; 是首项为
是首项为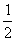 ,公比为
,公比为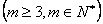 ,并对任意
,并对任意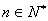 ,均有
,均有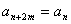 成立,
成立,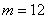 时,求
时,求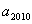 ;
; 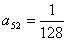 ,试求
,试求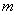 的值;
的值;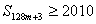 成立,若存在,求出
成立,若存在,求出