Question

(1)不等式的解为＜x＜1,求a、b的值.

(2)k为何值时，不等式0＜≤6对任意实数x恒成立？

Answer 1

解析：(1)∵x∈R,x²+x+1和x²-x+1恒正,∴原不等式可化为（x-a）(x²-x+1)＞(x-b)(x²+x+1),即化为(a-b+2)x²-(a+b)x+(a-b)x＜0.

记f(x)=(a-b+2)x²-(a+b)x+(a-b),

由于题中不等式解集为（，1）.

∴，1是f(x)=0的两根.

∴

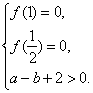
解得a=4,b=2.

(2)∵x²-x+1＞0,

∴

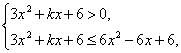
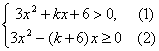∴恒成立，

由①得Δ₁=k²-72＜0.

∴-6＜k＜6                                        ③

由②得Δ₂=（k+6）²≤0.∴k=-6.                      ④

③④取交集得k=-6.