题目内容
已知椭圆 的两个焦点
的两个焦点 和上下两个顶点
和上下两个顶点 是一个边长为2且∠F1B1F2为
是一个边长为2且∠F1B1F2为 的菱形的四个顶点.
的菱形的四个顶点.
(1)求椭圆 的方程;
的方程;
(2)过右焦点F2
,斜率为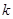 (
(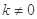 )的直线
)的直线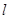 与椭圆
与椭圆 相交于
相交于 两点,A为椭圆的右顶点,直线
两点,A为椭圆的右顶点,直线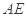 、
、 分别交直线
分别交直线 于点
于点 、
、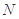 ,线段
,线段 的中点为
的中点为 ,记直线
,记直线 的斜率为
的斜率为 .求证:
.求证: 为定值.
为定值.
【答案】
(1)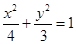 ;(2)
;(2)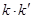 为定值
为定值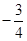 .
.
【解析】
试题分析:(1)由椭圆两个焦点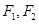 和上下两个顶点
和上下两个顶点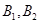 是一个边长为2且∠F1B1F2为
是一个边长为2且∠F1B1F2为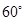 的菱形的四个顶点可得
的菱形的四个顶点可得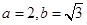 ,从而得到椭圆方程.(2)通过题目条件,将直线
,从而得到椭圆方程.(2)通过题目条件,将直线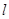 方程设出来,再将它与椭圆交点坐标设出来,即点
方程设出来,再将它与椭圆交点坐标设出来,即点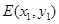 ,点
,点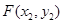 ,再分别表示出直线
,再分别表示出直线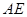 、
、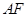 的方程,令
的方程,令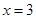 ,得到点
,得到点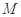 ,
,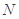 ,的坐标,再利用中点坐标公式得到线段
,的坐标,再利用中点坐标公式得到线段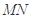 的中点为
的中点为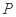 的坐标,利用斜率公式即得到
的坐标,利用斜率公式即得到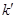 ,通过联立直线
,通过联立直线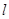 与椭圆方程,用韦达定理替换
与椭圆方程,用韦达定理替换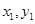 ,
,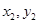 ,化简之后即可证明
,化简之后即可证明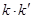 为定值.本题利用“设而不求”达到证明的目的,充分利用韦达定理消去繁杂的未知数.这是解决带有直线与圆锥曲线交点问题的常用的手段.
为定值.本题利用“设而不求”达到证明的目的,充分利用韦达定理消去繁杂的未知数.这是解决带有直线与圆锥曲线交点问题的常用的手段.
试题解析:(1)由条件知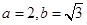 , 2分
, 2分
故所求椭圆方程为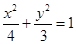 . 4分
. 4分
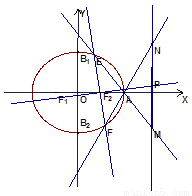
(2)设过点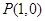 的直线
的直线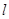 方程为:
方程为: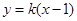 ,设点
,设点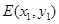 ,点
,点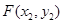 ,
,
将直线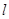 方程
方程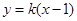 代入椭圆
代入椭圆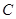 :
: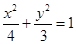 ,
,
整理得: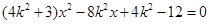 , 6分
, 6分
因为点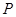 在椭圆内,所以直线
在椭圆内,所以直线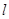 和椭圆都相交,
和椭圆都相交,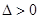 恒成立,且
恒成立,且
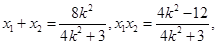 8分
8分
直线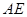 的方程为:
的方程为: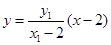 ,直线
,直线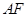 的方程为:
的方程为: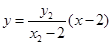 ,令
,令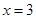 ,
,
得点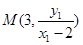 ,
,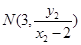 ,所以点
,所以点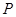 的坐标
的坐标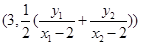 . 9分
. 9分
直线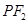 的斜率为
的斜率为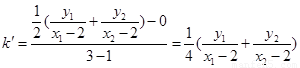 .
.
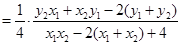
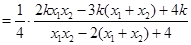 . 11分
. 11分
将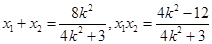 代入上式得:
代入上式得:
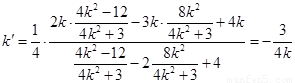 .
.
所以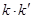 为定值
为定值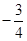 . 14分
. 14分
考点:1.椭圆的简单几何性质;2.直线与圆锥曲线的位置关系;3.斜率公式及直线方程.

练习册系列答案
相关题目
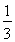
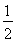
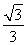
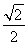
 的两个焦点为F1(-c,0)、F2(c,0),c2是a2与b2的等差中项,其中a、b、c都是正数,过点A(0,-b)和B(a,0)的直线与原点的距离为
的两个焦点为F1(-c,0)、F2(c,0),c2是a2与b2的等差中项,其中a、b、c都是正数,过点A(0,-b)和B(a,0)的直线与原点的距离为 .
. 的两个焦点为F1(-c,0)、F2(c,0),c2是a2与b2的等差中项,其中a、b、c都是正数,过点A(0,-b)和B(a,0)的直线与原点的距离为
的两个焦点为F1(-c,0)、F2(c,0),c2是a2与b2的等差中项,其中a、b、c都是正数,过点A(0,-b)和B(a,0)的直线与原点的距离为 .
.