题目内容
点(-2,-1)在直线x-y+c=0下方,则c的取值范围为
(1,+∞)
(1,+∞)
.分析:因为点(-2,-1)在直线x-y+c=0下方,所以可在直线x-y+c=0上取与点(-2,-1)横坐标相同的点,再比较两点的纵坐标即可.
解答:解:对于直线x-y+c=0,令x=-2,得,y=c-2,∴直线x-y+c=0上有点(-2,c-2),
∵点(-2,-1)在直线x-y+c=0下方,∴c-2>-1,c>1
故答案为(1,+∞)
∵点(-2,-1)在直线x-y+c=0下方,∴c-2>-1,c>1
故答案为(1,+∞)
点评:本题考查了二元一次不等式表示直线某一侧区域,做题适应认真分析点与直线位置关系.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
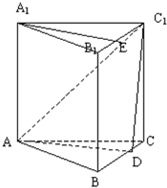 17、如图,在直三棱柱ABC-A1B1C1中,点D在BC上,AD⊥C1D,
17、如图,在直三棱柱ABC-A1B1C1中,点D在BC上,AD⊥C1D, 如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,
如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,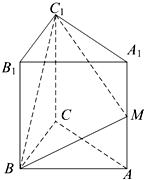 在直三棱柱ABC-A1B1C1中,AC=BC=2,AA1=2
在直三棱柱ABC-A1B1C1中,AC=BC=2,AA1=2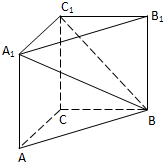 (2012•嘉定区三模)如图,在直三棱柱ABC-A1B1C1中,AC=BC=2且AC⊥BC,直线A1B与平面BCC1B1所成角的大小为arcsin
(2012•嘉定区三模)如图,在直三棱柱ABC-A1B1C1中,AC=BC=2且AC⊥BC,直线A1B与平面BCC1B1所成角的大小为arcsin 如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,
如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,